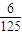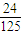题目内容
某学生在参加政、史、地三门课程的学业水平考试中,取得A等级的概率分别为 、
、 、
、 ,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为________.
,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为________.
| ξ | 0 | 1 | 2 | 3 |
| P | 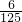 | a | b | 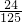 |

分析:①学生在参加政、史、地三门课程的学业水平考试中,有两门取得A等级有以下3种情况:政、史;政、地;地、史.再利用相互独立事件的概率计算公式、互斥事件的概率计算公式即可得到P(ξ=2);②根据概率的规范性可得:P(ξ=1)=1-P(ξ=0)-P(ξ=2)-P(ξ=3),据此即可得出P(ξ=1).利用离散型随机变量的数学期望即可得出Eξ.
解答:①学生在参加政、史、地三门课程的学业水平考试中,有两门取得A等级有以下3种情况:政、史;政、地;地、史.
∴P(ξ=2)=
 +
+ =
=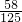 ,
,②根据分布列的性质可得:P(ξ=1)=1-P(ξ=0)-P(ξ=2)-P(ξ=3)=
 =
=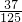 ,
,∴Eξ=0×
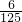 +
+ =
= =
= .
.故答案为
 .
.点评:熟练掌握相互独立事件的概率计算公式、互斥事件的概率计算公式、离散型随机变量的数学期望是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某学生在参加政、史、地三门课程的学业水平考试中,取得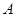 等级的概率分别为
等级的概率分别为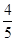 、
、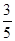 、
、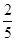 ,且三门课程的成绩是否取得
,且三门课程的成绩是否取得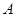 等级相互独立.
等级相互独立.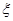 为该生取得
为该生取得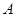 等级的课程数,其分布列如表所示,则数学期望
等级的课程数,其分布列如表所示,则数学期望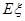 的值为______________.
的值为______________.
|
|
|
1 |
|
|
|
|
|
|
|
|
某学生在参加政、史、地三门课程的学业水平考试中,取得A等级的概率分别为 、
、 、
、 ,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为 .
,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为 .
 、
、 、
、 ,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为 .
,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为 .| ξ | 1 | 2 | 3 | |
| P |  | a | b |  |









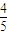 、
、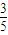 、
、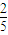 ,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为 .
,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为 .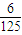
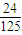
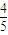 、
、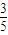 、
、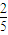 ,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为 .
,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望Eξ的值为 .