题目内容
实数列a,a1,a2,a3…,由下述等式定义 .
.(Ⅰ)若a为常数,求a1,a2,a3的值;
(Ⅱ)求依赖于a和n的an表达式;
(Ⅲ)求a的值,使得对任何正整数n总有an+1>an成立.
【答案】分析:(Ⅰ)利用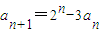 ,代入求解即可;
,代入求解即可;
(Ⅱ)由 ,得
,得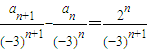 ,令
,令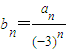 ,所以
,所以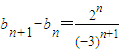 ,利用叠加法,可得
,利用叠加法,可得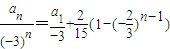 ,从而可得结论;
,从而可得结论;
(Ⅲ)先得出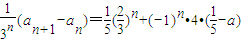 ,再对
,再对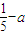 进行分类讨论,从而可得结论.
进行分类讨论,从而可得结论.
解答:解:(Ⅰ)∵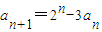 ,∴a1=1-3a,a2=-1+9a,a3=7-27a…(2分)
,∴a1=1-3a,a2=-1+9a,a3=7-27a…(2分)
(Ⅱ)由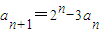 ,得
,得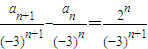 …(3分)
…(3分)
令 ,所以
,所以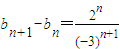
所以bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=
=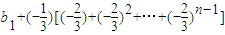 =
=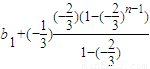
=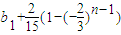 ,…(6分)
,…(6分)
所以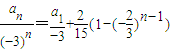 …(7分)
…(7分)
所以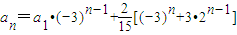 =
=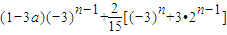
=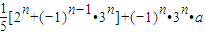 …(8分)
…(8分)
(Ⅲ)∵
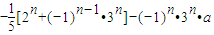
=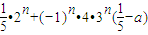
∴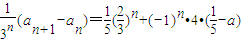 …(10分)
…(10分)
如果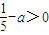 ,利用n无限增大时,
,利用n无限增大时,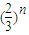 的值接近于零,对于非常大的奇数n,有an+1-an<0;
的值接近于零,对于非常大的奇数n,有an+1-an<0;
如果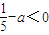 ,对于非常大的偶数n,an+1-an<0,不满足题目要求.
,对于非常大的偶数n,an+1-an<0,不满足题目要求.
当 时,
时,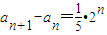 ,于是对于任何正整数n,an+1>an,因此
,于是对于任何正整数n,an+1>an,因此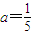 即为所求.…(13分)
即为所求.…(13分)
点评:本题考查数列递推式,考查数列通项的研究,考查恒成立问题,确定数列的通项是关键.
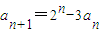 ,代入求解即可;
,代入求解即可;(Ⅱ)由
 ,得
,得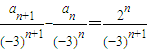 ,令
,令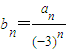 ,所以
,所以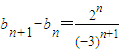 ,利用叠加法,可得
,利用叠加法,可得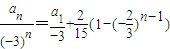 ,从而可得结论;
,从而可得结论;(Ⅲ)先得出
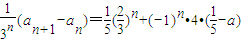 ,再对
,再对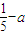 进行分类讨论,从而可得结论.
进行分类讨论,从而可得结论.解答:解:(Ⅰ)∵
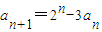 ,∴a1=1-3a,a2=-1+9a,a3=7-27a…(2分)
,∴a1=1-3a,a2=-1+9a,a3=7-27a…(2分)(Ⅱ)由
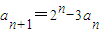 ,得
,得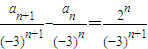 …(3分)
…(3分)令
 ,所以
,所以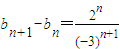
所以bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=

=
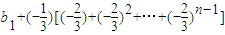 =
=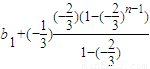
=
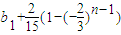 ,…(6分)
,…(6分)所以
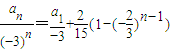 …(7分)
…(7分)所以
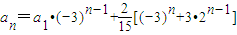 =
=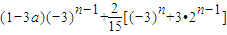
=
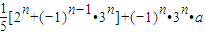 …(8分)
…(8分)(Ⅲ)∵

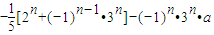
=
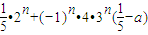
∴
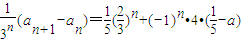 …(10分)
…(10分)如果
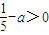 ,利用n无限增大时,
,利用n无限增大时,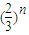 的值接近于零,对于非常大的奇数n,有an+1-an<0;
的值接近于零,对于非常大的奇数n,有an+1-an<0;如果
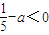 ,对于非常大的偶数n,an+1-an<0,不满足题目要求.
,对于非常大的偶数n,an+1-an<0,不满足题目要求.当
 时,
时,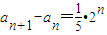 ,于是对于任何正整数n,an+1>an,因此
,于是对于任何正整数n,an+1>an,因此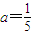 即为所求.…(13分)
即为所求.…(13分)点评:本题考查数列递推式,考查数列通项的研究,考查恒成立问题,确定数列的通项是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 ,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.
,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.