题目内容
若点（x0，y0）在椭圆
+
=1内部，则有
+
＜1，问直线
+
=1与椭圆的交点个数是
| x2 |
| a2 |
| y2 |
| b2 |
| x02 |
| a2 |
| y02 |
| b2 |
| xx0 |
| a2 |
| yy0 |
| b2 |
0
0
．分析：判断直线与椭圆的位置关系只能将直线方程和椭圆方程联立，通过所得关于x的一元二次方程的判别式的正负判断直线与椭圆的位置关系，注意在变形中利用已知
+
＜1
| x02 |
| a2 |
| y02 |
| b2 |
解答：解：将直线
+
=1代入椭圆方程
+
=1得：
+b2(
-
) 2=1
即(
)x2-
x+
=0
∵△=
-4×(
)×
=
=
∵
+
＜1，
∴-a2b2+a2y02+b2x02＜0
∴△＜0
∴直线与椭圆的交点个数为0
故答案为0
| xx0 |
| a2 |
| yy0 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| 1 |
| y0 |
| xx0 |
| a2y0 |
即(
| a2y02+b2x02 |
| a4y02 |
| 2b2x0 |
| a2y02 |
| b2-y02 |
| y02 |
∵△=
| 4b4x02 |
| a4y04 |
| a2y02+b2x02 |
| a4y02 |
| b2-y02 |
| y02 |
=
| 4(b4x02-a2b2y02+a2y04-b4x02+b2x02y02) |
| a4y04 |
=
| 4y02( -a2b2 +a2y02+b2x02 ) |
| a4y04 |
∵
| x02 |
| a2 |
| y02 |
| b2 |
∴-a2b2+a2y02+b2x02＜0
∴△＜0
∴直线与椭圆的交点个数为0
故答案为0
点评：本题考察了直线与椭圆的位置关系，通过联立方程组，利用一元二次方程根的判别式判断位置关系的方法，代数变形的能力
练习册系列答案
阅读快车系列答案
相关题目
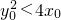，就叫点（x0，y0）在抛物线y2=4x的内部．若点（x0，y0）在抛物线y2=4x的内部，则直线y0y=2（x0+x）与抛物线y2=4x