题目内容
若点(x0,y0)满足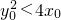 ,就叫点(x0,y0)在抛物线y2=4x的内部.若点(x0,y0)在抛物线y2=4x的内部,则直线y0y=2(x0+x)与抛物线y2=4x
,就叫点(x0,y0)在抛物线y2=4x的内部.若点(x0,y0)在抛物线y2=4x的内部,则直线y0y=2(x0+x)与抛物线y2=4x
- A.有一个公共点
- B.至少有一个公共点
- C.恰有两个公共点
- D.无公共点
D
分析:将直线方程与抛物线方程联立,消去x,求出方程的判别式,利用点(x0,y0)在抛物线y2=4x的内部,判断判别式小于0,从而可得结论.
解答:由y0y=2(x0+x)可得 ,代入抛物线y2=4x
,代入抛物线y2=4x
即y2=2y0y-4x0
∴y2-2y0y+4x0=0
∴ =4(
=4( )
)
∵点(x0,y0)在抛物线y2=4x的内部
∴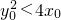
∴ <0
<0
∴△<0
∴直线y0y=2(x0+x)与抛物线y2=4x无公共点
故选D.
点评:本题以新定义为载体,考查学生对新定义的理解,考查直线与抛物线的位置关系,解题的关键是直线与抛物线方程的联立.
分析:将直线方程与抛物线方程联立,消去x,求出方程的判别式,利用点(x0,y0)在抛物线y2=4x的内部,判断判别式小于0,从而可得结论.
解答:由y0y=2(x0+x)可得
 ,代入抛物线y2=4x
,代入抛物线y2=4x即y2=2y0y-4x0
∴y2-2y0y+4x0=0
∴
 =4(
=4( )
)∵点(x0,y0)在抛物线y2=4x的内部
∴
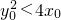
∴
 <0
<0∴△<0
∴直线y0y=2(x0+x)与抛物线y2=4x无公共点
故选D.
点评:本题以新定义为载体,考查学生对新定义的理解,考查直线与抛物线的位置关系,解题的关键是直线与抛物线方程的联立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目