Question

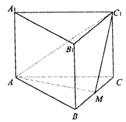
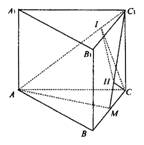
（08年潍坊市六模） （12分）如图，正三棱柱的底面边长为a，点M在边BC上，△是以点M为直角顶点的等腰直角三角形．

 

　　（1）求证点M为边BC的中点；

　　（2）求点C到平面的距离；

　　（3）求二面角的大小．

　

Answer 1

解析：（甲）（1）∵　△为以点M为直角顶点的等腰直角三角形，∴　且．

　　∵　正三棱柱，　∴　底面ABC．

　　∴　在底面内的射影为CM，AM⊥CM．

　　∵　底面ABC为边长为a的正三角形，　∴　点M为BC边的中点．

 

　　（2）过点C作CH⊥，由（1）知AM⊥且AM⊥CM，

　　∴　AM⊥平面　∵　CH在平面内，　∴　CH⊥AM，

　　∴　CH⊥平面，由（1）知，，且．

　　∴　．　∴　．

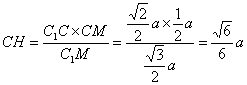　　∴　点C到平面的距离为底面边长为．

　　（3）过点C作CI⊥于I，连HI，　∵　CH⊥平面，

　　∴　HI为CI在平面内的射影，

　　∴　HI⊥，∠CIH是二面角的平面角．

　　在直角三角形中，，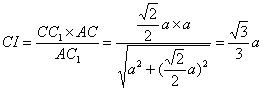

，

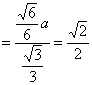　　∴　∠CIH＝45°，　∴　二面角的大小为45°