题目内容
已知虚数z满足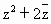 ∈R,arg(3-z)=
∈R,arg(3-z)= ,解关于实数a的不等式:
,解关于实数a的不等式:
 (a>0且a≠1)
(a>0且a≠1)
答案:
解析:
解析:
|
解:设z=x+yi(x、y∈R,y≠0) 则 ∵ ∵ 将z=1-2i代入已知不等式得: 即: ①当a>1时,有 ②当0<a<1时,有 综上,原不等式的解集为:{a|0<a<1}
|

练习册系列答案
相关题目

 ∈R ∴2y(x-1)=0 ∵y≠0 ∴x=1 即z=1+yi
∈R ∴2y(x-1)=0 ∵y≠0 ∴x=1 即z=1+yi

 此不等式组无解
此不等式组无解 解得a∈(0,1)
解得a∈(0,1)