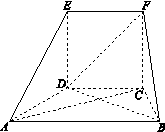
题目内容
如图所示,平面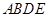 ⊥平面
⊥平面 ,
, ,
,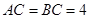 ,四边形
,四边形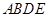 是直角梯形,
是直角梯形,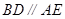 ,
,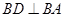 ,
,  ,
, 分别为
分别为 的中点.
的中点. 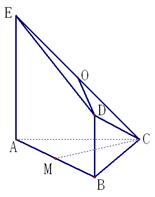
(Ⅰ) 用几何法证明: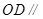 平面
平面 ;
;
(Ⅱ)用几何法证明: 平面
平面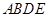 .
.
(1)利用三角形的中位线的性质,先证明四边形ODBF是平行四边形,从而可得OD∥FB,利用线面平行的判定,可以证明OD∥平面ABC;(2)利用平面ABDE⊥平面ABC,证明BD⊥平面ABC,进而可证 平面ABDE;
平面ABDE;
解析试题分析:(Ⅰ)证明:取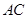 中点
中点 ,连结
,连结 . ∵
. ∵ 是
是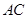 的中点,
的中点, 为
为 的中点,
的中点,
∴ 且
且 , 又
, 又 且
且 ,
,
∴ ,
,
∴四边形 是平行四边形.
是平行四边形.
∴ 4分
4分
又∵ 平面
平面 ,
, 平面
平面 ,
,
∴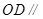 平面
平面 . 6分
. 6分
(Ⅱ)证明: ,
, 为
为 中点,∴
中点,∴ , 8分
, 8分
又∵面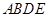 ⊥面
⊥面 ,面
,面
 面
面 ,
, 面
面 ,
,
∴ 面
面 . 12分
. 12分
考点:线面平行,线面垂直
点评:本题考查线面平行,考查线面垂直,考查线面角,解题的关键是正确运用线面平行与垂直的判定与性质,正确运用向量法求线面角.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 ,AE、CF都与平面ABCD垂直,AE=1,CF=2.
,AE、CF都与平面ABCD垂直,AE=1,CF=2.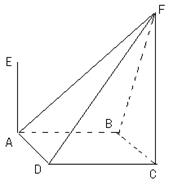

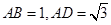 ,
,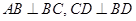 ,如图(1).把
,如图(1).把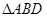 沿
沿 翻折,使得平面
翻折,使得平面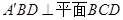 ,如图(2).
,如图(2).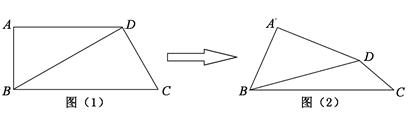
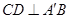 ;
; 的体积;
的体积;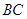 上是否存在点N,使得
上是否存在点N,使得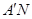
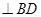 ?若存在,请求出
?若存在,请求出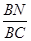 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.  ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。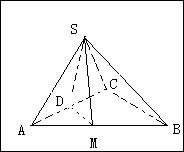
 ABC=
ABC=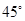 ,AB=2
,AB=2 ,BC=2AE=4,
,BC=2AE=4, 是等腰三角形.
是等腰三角形.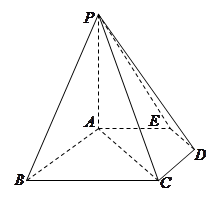
 的三视图如图所示,
的三视图如图所示,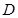 是
是 的中点.
的中点.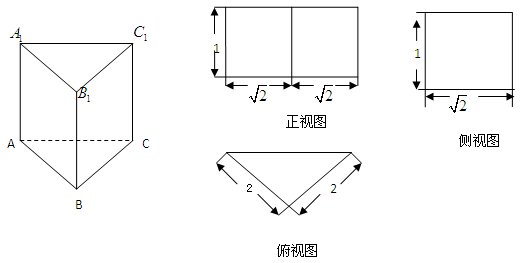
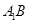 ∥平面
∥平面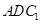 ;
;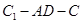 的余弦值;
的余弦值;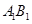 上是否存在点
上是否存在点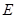 ,使
,使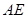 与
与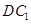 成
成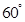 角?若存在,确定
角?若存在,确定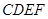 为正方形,面
为正方形,面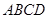 为等腰梯形,
为等腰梯形,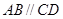 ,
,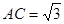 ,
,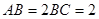 ,
,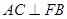 .
.
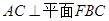 ;
;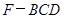 的体积;
的体积; 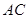 上是否存在点
上是否存在点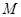 ,使
,使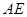 //平面
//平面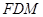 ?证明你的结论.
?证明你的结论. 中,
中,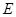 是
是 的中点.
的中点.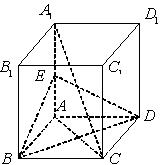
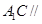 平面
平面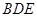 ;
;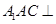 平面
平面