Question

在△ABC中，∠C=90°，则cos²A+cos²B=1，用类比的方法猜想三棱锥的类似性质，并证明你的猜想．

Answer 1

考点：棱锥的结构特征,类比推理

专题：空间位置关系与距离

分析：“在三棱锥P-ABC中，三个侧面PAB、PAC、PCB两两垂直，且与底面所成的角分别为α，β，γ，则cos²α+cos²β+cos²γ=1”．
证明：设P在平面ABC上的射影为O，记PO=h，由已知得cosα=sin∠PCO=

h

PC

，同理，cosβ=

h

PA

，cosγ=

h

PB

，由此能证明cos²α+cos²β+cos²γ=1．

解答： 解：如图，由平面类比到空间，有下列猜想：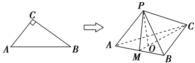
“在三棱锥P-ABC中，三个侧面PAB、PAC、PCB两两垂直，且与底面所成的角分别为α，β，γ，则cos²α+cos²β+cos²γ=1”．
证明：设P在平面ABC上的射影为O，记PO=h，
∵PC⊥PA，PC⊥pB，∴PC⊥平面PAB，
∴PC⊥PM，（M为CO与AB的交点），且∠PMC=α，
cosα=sin∠PCO=

h

PC

，
同理，cosβ=

h

PA

，cosγ=

h

PB

，
又

1

6

PA•PB•PC=VP-ABC=

1

3

(S△AOB+S△BOC+S△COA)h
=

1

3

(

1

2

PA•PB•cosα+

1

2

PB•PCcosβ+

1

2

PB•PCcosγ)h，
∴(

cosα

PC

+

cosβ

PA

+

cosγ

PB

)h=1，
∴cos²α+cos²β+cos²γ=1．

点评：本题考查类比的方法猜想三棱锥的类似性质，并证明猜想，是中档题，解题时要注意空间思维能力的培养．