题目内容
下列命题正确的是
①动点M至两定点A、B的距离之比为常数λ(λ>0且λ≠1).则动点M的轨迹是圆.
②椭圆 为半焦距).
为半焦距).
③双曲线 的焦点到渐近线的距离为b.
的焦点到渐近线的距离为b.
④已知抛物线y2=2px上两点A(x1,y1),B(x2,y2)且OA⊥OB(O为原点),则y1y2=-p2.
- A.②③④
- B.①④
- C.①②③
- D.①③
C
分析:①由圆的性质知此命题成立;②若椭圆的离心率 ,则这个椭圆是等轴双曲线,所以②成立;③双曲线
,则这个椭圆是等轴双曲线,所以②成立;③双曲线 的焦点到渐近线的距离
的焦点到渐近线的距离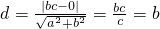 .故③成立.④已知抛物线y2=2px上两点A(x1,y1),B(x2,y2)且OA⊥OB(O为原点),则y1y2=-4p2.故④不成立.
.故③成立.④已知抛物线y2=2px上两点A(x1,y1),B(x2,y2)且OA⊥OB(O为原点),则y1y2=-4p2.故④不成立.
解答:①动点M至两定点A、B的距离之比为常数λ(λ>0且λ≠1).则动点M的轨迹是圆.由圆的性质知此命题成立.
②若椭圆的离心率 ,则这个椭圆是等轴双曲线,所以②成立.
,则这个椭圆是等轴双曲线,所以②成立.
③∵双曲线 的一个焦点是(c,0),相应的渐近线方程是bx-ay=0,
的一个焦点是(c,0),相应的渐近线方程是bx-ay=0,
∴双曲线 的焦点到渐近线的距离
的焦点到渐近线的距离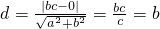 .
.
故③成立.
④已知抛物线y2=2px上两点A(x1,y1),B(x2,y2)且OA⊥OB(O为原点),则y1y2=-4p2.故④不成立.
故选C.
点评:本题考查圆锥曲线的性质和应用,解题时要熟练掌握圆曲线的基本性质.
分析:①由圆的性质知此命题成立;②若椭圆的离心率
 ,则这个椭圆是等轴双曲线,所以②成立;③双曲线
,则这个椭圆是等轴双曲线,所以②成立;③双曲线 的焦点到渐近线的距离
的焦点到渐近线的距离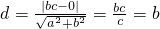 .故③成立.④已知抛物线y2=2px上两点A(x1,y1),B(x2,y2)且OA⊥OB(O为原点),则y1y2=-4p2.故④不成立.
.故③成立.④已知抛物线y2=2px上两点A(x1,y1),B(x2,y2)且OA⊥OB(O为原点),则y1y2=-4p2.故④不成立.解答:①动点M至两定点A、B的距离之比为常数λ(λ>0且λ≠1).则动点M的轨迹是圆.由圆的性质知此命题成立.
②若椭圆的离心率
 ,则这个椭圆是等轴双曲线,所以②成立.
,则这个椭圆是等轴双曲线,所以②成立.③∵双曲线
 的一个焦点是(c,0),相应的渐近线方程是bx-ay=0,
的一个焦点是(c,0),相应的渐近线方程是bx-ay=0,∴双曲线
 的焦点到渐近线的距离
的焦点到渐近线的距离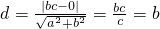 .
.故③成立.
④已知抛物线y2=2px上两点A(x1,y1),B(x2,y2)且OA⊥OB(O为原点),则y1y2=-4p2.故④不成立.
故选C.
点评:本题考查圆锥曲线的性质和应用,解题时要熟练掌握圆曲线的基本性质.

练习册系列答案
相关题目
 (2013•安徽)如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是
(2013•安徽)如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是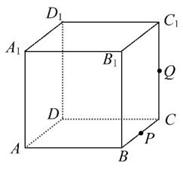 ①当0<CQ<
①当0<CQ< 的棱长为1,
的棱长为1,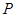 为
为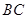 的中点,
的中点,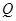 为线段
为线段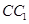 上的动点,过点
上的动点,过点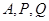 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为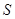 ,则下列命题正确的是 (写出所有正确命题的编号)。
,则下列命题正确的是 (写出所有正确命题的编号)。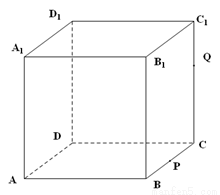
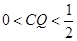 时,
时,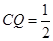 时,
时,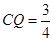 时,
时,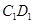 的交点
的交点 满足
满足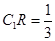
 时,
时,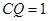 时,
时,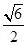
 .则动点M的轨迹是圆。
.则动点M的轨迹是圆。 为半焦距)。
为半焦距)。 的焦点到渐近线的距离为b。
的焦点到渐近线的距离为b。