题目内容
已知向量 的模为2,向量
的模为2,向量 为单位向量,
为单位向量,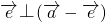 ,则向量
,则向量 与
与 的夹角大小为________.
的夹角大小为________.

分析:设向量
 与
与 的夹角为θ,可得
的夹角为θ,可得 •
• =2cosθ,再根据
=2cosθ,再根据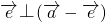 ,得
,得 •
• -
- 2=2cosθ-1=0,最后结合θ∈[0,π],可得向量
2=2cosθ-1=0,最后结合θ∈[0,π],可得向量 与
与 的夹角θ的大小.
的夹角θ的大小.解答:设向量
 与
与 的夹角为θ,
的夹角为θ,∴
 •
• =
= •
• cosθ=1×2×cosθ=2cosθ
cosθ=1×2×cosθ=2cosθ∵
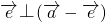 ,
,∴
 =
= •
• -
- 2=0,得2cosθ-1=0,所以cosθ=
2=0,得2cosθ-1=0,所以cosθ= ,
,∵θ∈[0,π],∴θ=

故答案为:

点评:本题给出单位向量
 与向量
与向量 的差向量垂直于单位向量
的差向量垂直于单位向量 ,求
,求 与
与 的夹角大小,着重考查了平面向量的数量积运算和向量的夹角等知识,属于基础题.
的夹角大小,着重考查了平面向量的数量积运算和向量的夹角等知识,属于基础题. 
练习册系列答案
相关题目
 的同向单位向量为
的同向单位向量为 =(
=( ,
, ),若向量
),若向量 的起点坐标为(1,-2),模为4
的起点坐标为(1,-2),模为4 ,则
,则 的终点坐标是
的终点坐标是 -2)
-2) ,4)
,4)  -2)或(7,-2-2
-2)或(7,-2-2 )
)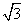 ,-6)
,-6)