题目内容
3.计算:sin$\frac{29π}{6}$+cos(-$\frac{29π}{3}$)-tan$\frac{25π}{4}$=-$\frac{\sqrt{3}+1}{2}$.分析 利用诱导公式化简后,根据特殊角的三角函数值即可求值得解.
解答 解:sin$\frac{29π}{6}$+cos(-$\frac{29π}{3}$)-tan$\frac{25π}{4}$=sin$\frac{5π}{6}$+cos$\frac{5π}{6}$-tan$\frac{π}{4}$=$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$-1=-$\frac{\sqrt{3}+1}{2}$.
故答案为:-$\frac{\sqrt{3}+1}{2}$.
点评 本题主要考查了诱导公式,特殊角的三角函数值的应用,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
13.函数f(x)=lnx+$\frac{1}{x}$-2 的零点个数为( )
| A. | 0个 | B. | 1个 | C. | 2 个 | D. | 3 个 |
14.已知a=0.71.3,b=30.2,c=log0.25,则a、b、c之间的大小关系为( )
| A. | a<c<b | B. | c<b<a | C. | b<c<a | D. | c<a<b |
11.函数f(x)=-2x2+ax+1在($\frac{1}{2},+∞$)是减函数,则a的取值范围是( )
| A. | ($-∞,\frac{1}{2}$) | B. | (-∞,2] | C. | [4,+∞) | D. | (-∞,-2] |
12.已知$\sqrt{2}$,a+1,2$\sqrt{2}$成等比数列,则a的值为( )
| A. | -3 | B. | 1 | C. | -1或3 | D. | -3或1 |
13.设f(x)=lnx,0<a<b,若$p=f(\sqrt{ab})$,$q=f(\frac{a+b}{2})$,r=$\frac{f(a)+f(b)}{2}$,则下列关系式中正确的是( )
| A. | p=r<q | B. | q=r>p | C. | p=r>q | D. | q=r<p |
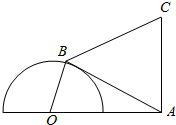 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC,设∠AOB=α.问:当α取何值时,四边形OACB面积最大?
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC,设∠AOB=α.问:当α取何值时,四边形OACB面积最大?