题目内容
（2013•泉州模拟）如图所示的三个等腰直角三角形是某几何体的三视图，则该几何体的外接球的表面积为3π
3π
．分析：由题意可知三视图复原的几何体是三棱锥，正方体的一个角，根据三视图的数据，求出三棱锥的外接球的表面积即可．
解答：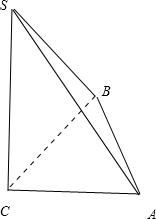
解：由几何体的三视图知，
几何体如图所示的三棱锥，
∵几何体的三视图均为腰长为1的等腰直角三角形，
∴SC=AC=BC=1，
且∠SCA=∠SCB=∠ACB=90°，
∵它是棱长为1的正方体的一个角，
∴它的外接球就是棱长为1的正方体的外接球，
外接球的半径R=
，
∴外接球的表面积S=4π（
）2=3π．
故答案为：3π．
解：由几何体的三视图知，几何体如图所示的三棱锥，
∵几何体的三视图均为腰长为1的等腰直角三角形，
∴SC=AC=BC=1，
且∠SCA=∠SCB=∠ACB=90°，
∵它是棱长为1的正方体的一个角，
∴它的外接球就是棱长为1的正方体的外接球，
外接球的半径R=
| ||
| 2 |
∴外接球的表面积S=4π（
| ||
| 2 |
故答案为：3π．
点评：本题考查由三视图求几何体的表面积，考查由三视图还原直观图形，考查三棱锥的外接球的表面积，本题是一个基础题．
练习册系列答案
相关题目
（2013•泉州模拟）如图，等腰梯形ABCD中，AB∥CD且AB=2，AD=1，DC=2x（x∈（0，1））．以A，B为焦点，且过点D的双曲线的离心率为e1；以C，D为焦点，且过点A的椭圆的离心率为e2，则e1+e2的取值范围为 （ ）
（2013•泉州模拟）设全集U=R，A={x|x（x+3）＜0}，B={x|x＜-1}，则图中阴影部分表示的集合为（ ）