题目内容
已知a为实数,p:点M(1,1)在圆(x+a)2+(y-a)2=4的内部; q:?x∈R,都有x2+ax+1≥0.
(1)若p为真命题,求a的取值范围;
(2)若q为假命题,求a的取值范围;
(3)若“p且q”为假命题,且“p或q”为真命题,求a的取值范围.
(1)若p为真命题,求a的取值范围;
(2)若q为假命题,求a的取值范围;
(3)若“p且q”为假命题,且“p或q”为真命题,求a的取值范围.
分析:对于命题p为真,要利用点与圆的位置关系;对于命题q为真,要利用一元二次函数图象的特点,最后利用复合命题真假解决.
解答:解:(1)∵p:点M(1,1)在圆(x+a)2+(y-a)2=4的内部
∴(1+a)2+(1-a)2<4,解得-1<a<1,
故p为真命题时a的取值范围为(-1,1).
(2)∵q:?x∈R,都有x2+ax+1≥0
∴若q为真命题,则△=a2-4≤0,解得-2≤a≤2,
故q为假命题时a的取值范围(-∞,-2)∪(2,+∞).
(3)∵“p且q”为假命题,且“p或q”为真命题
∴p与q一真一假,从而
①当p真q假时有
,无解;
②当p假q真时有
,解得-2≤a≤-1或1≤a≤2.
∴实数a的取值范围是[-2,-1]∪[1,2].
∴(1+a)2+(1-a)2<4,解得-1<a<1,
故p为真命题时a的取值范围为(-1,1).
(2)∵q:?x∈R,都有x2+ax+1≥0
∴若q为真命题,则△=a2-4≤0,解得-2≤a≤2,
故q为假命题时a的取值范围(-∞,-2)∪(2,+∞).
(3)∵“p且q”为假命题,且“p或q”为真命题
∴p与q一真一假,从而
①当p真q假时有
|
②当p假q真时有
|
∴实数a的取值范围是[-2,-1]∪[1,2].
点评:此题考查复合命题真假,此外考查点与圆的位置关系的判别,一元二次函数等问题.

练习册系列答案
相关题目
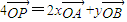 ,则
,则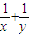 的最小值为 .
的最小值为 .