题目内容
若 ,则
,则 的最小值为 .
的最小值为 .
4
解析试题分析: ,
, ,
, ,当
,当 即
即 时等号成立,所以
时等号成立,所以 的最小值为4.
的最小值为4.
考点:基本不等式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各式中,最小值等于2的是( )
A. | B. |
C. | D. |
当x>1时,不等式x-2+ ≥
≥ 恒成立,则实数
恒成立,则实数 的取值范围是 ( )
的取值范围是 ( )
| A.(-∞,0] | B.[0,+∞) | C.[1,+∞) | D.(-∞,1] |
在直角坐标系中,定义两点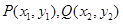 之间的“直角距离”为
之间的“直角距离”为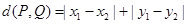 ,
,
现给出四个命题:
①已知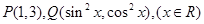 ,则
,则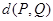 为定值;
为定值;
②用 表示
表示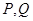 两点间的“直线距离”,那么
两点间的“直线距离”,那么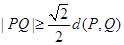 ;
;
③已知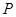 为直线
为直线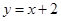 上任一点,
上任一点,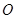 为坐标原点,则
为坐标原点,则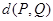 的最小值为
的最小值为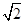 ;
;
④已知 三点不共线,则必有
三点不共线,则必有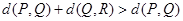 .
.
| A.②③ | B.①④ | C.①② | D.①②④ |
设 ,若直线
,若直线 与
与 轴相交于点
轴相交于点 ,与
,与 轴相交于点
轴相交于点 ,且坐标原点
,且坐标原点 到直线
到直线 的距离为
的距离为 ,则
,则 的面积
的面积 的最小值为
的最小值为
A.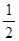 | B.2 | C.3 | D.4 |
设 、
、 为正数,则
为正数,则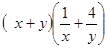 的最小值为( )
的最小值为( )
A. | B.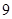 | C.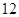 | D. |
已知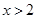 ,则函数
,则函数 的最小值是( )
的最小值是( )
| A.5 | B.4 | C.8 | D.6 |
若正数 满足
满足 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
设正实数 满足
满足 ,则当
,则当 取得最大值时,
取得最大值时, 的最大值为( )
的最大值为( )
A. | B. | C. | D. |