题目内容
8.写出函数f(x)=x+log2x的一个含有零点的区间($\frac{1}{2}$,1).分析 根据函数的实根存在定理,要验证函数的零点的位置,只要求出函数在区间的两个端点上的函数值,得到结果.
解答 解:∵f($\frac{1}{2}$)=$\frac{1}{2}$-1=-$\frac{1}{2}$,f(1)=1
∴f($\frac{1}{2}$)•f(1)<0,
∴根据函数的实根存在定理得到零点的区间是($\frac{1}{2}$,1).
故答案为:($\frac{1}{2}$,1).
点评 本题考查函数零点的判定定理,本题解题的关键是做出区间的两个端点的函数值,本题是一个基础题.

练习册系列答案
相关题目
16.设X~B(10,0.8)则k=( )时,P(x=k)最大.
| A. | 8 | B. | 9 | C. | 8或9 | D. | 7或8 |
13.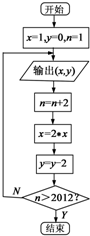 某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
 某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )| A. | 32 | B. | 24 | C. | 18 | D. | 16 |
20.不等式$\frac{({x}^{3}-1)(3-2x-{x}^{2})}{({x}^{2}+x-12)}$≤0的解集为( )
| A. | (-∞,-4)∪[-3,3) | B. | (-4,-3]∪{1}∪(3,+∞) | C. | (-∞,-3]∪{1}∪(3,+∞) | D. | [-3,3) |