题目内容
求证：
是无理数．
证明：假设是有理数，不妨设=
（p，q是互质的正整数）．
则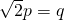
?q2=2p2，故2必是q的因数．
于是可设q=2m（m为正整数），则2p2=4m2，即p2=2m2，故2又是p的因数．
因此p，q有公因数2，这与p，q是互质的正整数相矛盾．
这说明假设是有理数不成立，故是无理数．
分析：利用反证法，假设是有理数，不妨设=（p，q是互质的正整数）．可得2必是q的因数，所以可设q=2m（m为正整数），从而可知2又是p的因数，因此p，q有公因数2，这与p，q是互质的正整数相矛盾．从而问题得证．
点评：本题的考点是反证法，主要考查反证法的运用，解题的关键是利用反证法的证题步骤：反设，归谬，引出矛盾，从而下结论．
是有理数，不妨设=（p，q是互质的正整数）．则
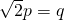?q2=2p2，故2必是q的因数．于是可设q=2m（m为正整数），则2p2=4m2，即p2=2m2，故2又是p的因数．
因此p，q有公因数2，这与p，q是互质的正整数相矛盾．
这说明假设
是有理数不成立，故是无理数．分析：利用反证法，假设
是有理数，不妨设=（p，q是互质的正整数）．可得2必是q的因数，所以可设q=2m（m为正整数），从而可知2又是p的因数，因此p，q有公因数2，这与p，q是互质的正整数相矛盾．从而问题得证．点评：本题的考点是反证法，主要考查反证法的运用，解题的关键是利用反证法的证题步骤：反设，归谬，引出矛盾，从而下结论．
练习册系列答案
相关题目
是无理数.