题目内容
 如图,两座建筑物AB,CD的高度分别为9m和15m,从建筑物AB的顶部看建筑物CD的张角∠CAD=45°.
如图,两座建筑物AB,CD的高度分别为9m和15m,从建筑物AB的顶部看建筑物CD的张角∠CAD=45°.
(1)求建筑物AB和CD的底部之间的距离BD;
(2)求∠ADB的正切值.
解:(1)如图作AE⊥CD于E.
∵AB∥CD,AB=9,CD=15,∴DE=9,EC=6.
设AE=x,∠CAE=α,
∵∠CAD=45°,∴∠DAE=45°-α.
在Rt△AEC和Rt△AED中,
∵tanα= ,tan(45°-α)=
,tan(45°-α)= 
∴ =tan(45°-α)=
=tan(45°-α)= 
∴ =
= ,化简整理得x2-15x-54=0,
,化简整理得x2-15x-54=0,
解得x1=18,x2=-3(舍去).
答:两建筑物底部间距离BD是18 m.
(2)由(1)可知BD=18,AB=9,所以tan∠ADB= =
= =
= .
.
∠ADB的正切值为: .
.
分析:(1)作AE⊥CD于E,问题转化为求△ACD边CD上的高.设AE=x,只要建立起关于x的方程,则问题可解.
(2)利用(1)直接求出∠ADB的正切值.
点评:本题主要考查了解三角形的实际应用.解这类题的关键是建立数学模型,设出恰当的角.考查两角和与差的三角函数,考查计算能力.
∵AB∥CD,AB=9,CD=15,∴DE=9,EC=6.
设AE=x,∠CAE=α,
∵∠CAD=45°,∴∠DAE=45°-α.
在Rt△AEC和Rt△AED中,
∵tanα=
 ,tan(45°-α)=
,tan(45°-α)= 
∴
 =tan(45°-α)=
=tan(45°-α)= 
∴
 =
= ,化简整理得x2-15x-54=0,
,化简整理得x2-15x-54=0,解得x1=18,x2=-3(舍去).
答:两建筑物底部间距离BD是18 m.
(2)由(1)可知BD=18,AB=9,所以tan∠ADB=
 =
= =
= .
.∠ADB的正切值为:
 .
.分析:(1)作AE⊥CD于E,问题转化为求△ACD边CD上的高.设AE=x,只要建立起关于x的方程,则问题可解.
(2)利用(1)直接求出∠ADB的正切值.
点评:本题主要考查了解三角形的实际应用.解这类题的关键是建立数学模型,设出恰当的角.考查两角和与差的三角函数,考查计算能力.

练习册系列答案
相关题目
 如图,两座建筑物AB,CD的高度分别是9m和15m,从建筑AB看建筑物CD的张角∠CAD=45°,求建筑物AB和CD的底部之间的距离BD.
如图,两座建筑物AB,CD的高度分别是9m和15m,从建筑AB看建筑物CD的张角∠CAD=45°,求建筑物AB和CD的底部之间的距离BD. (2013•徐州一模)如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.
(2013•徐州一模)如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.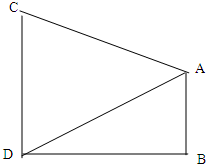 如图,两座建筑物AB,CD的高度分别为9m和15m,从建筑物AB的顶部看建筑物CD的张角∠CAD=45°.
如图,两座建筑物AB,CD的高度分别为9m和15m,从建筑物AB的顶部看建筑物CD的张角∠CAD=45°.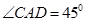 .
.
 ,
,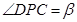 ,问点P在何处时,
,问点P在何处时,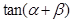 最小?
最小?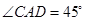 ,求建筑物AB和CD底部之间的距离BD
,求建筑物AB和CD底部之间的距离BD