题目内容

精英家教网如图是函数y=Asin（ωx+φ）+2的图象的一部分，它的振幅、周期、初相各是（　　）
A、A=3，T=
4π
3
，φ=-
π
6
B、A=1，T=
4π
3
，φ=-
3π
4
C、A=1，T=
2π
3
，φ=-
3π
4
D、A=1，T=
4π
3
，φ=-
π
6
分析：根据相邻最低与最高点的横坐标的差值是T的一半，求出T，再根据T=
2π
ω
求出ω，再根据最高点与最低点的纵坐标的差值是振幅的两倍，求出振幅，最后代入点（
π
6
，1）求出φ
解答：解：由图知周期T=
4
3
π，A=1，
又因为T=
2π
ω
，知ω=
3
2
；
再将点（
π
6
，1）代入y=Asin（ωx+φ）+2
计算求出φ=-
3
4
π，
故选B．
点评：此题容易对振幅和初相产生错误
练习册系列答案
相关题目
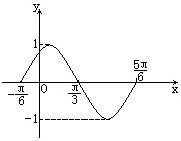精英家教网如图是函数y=Asin（ωx+φ）（A＜0，ω＞0，|φ|≤
π
2
）图象的一部分．为了得到这个函数的图象，只要将y=sinx（x∈R）的图象上所有的点（　　）
A、向左平移
π
3
个单位长度，再把所得各点的横坐标缩短到原来的
1
2
倍，纵坐标不变
B、向左平移
π
3
个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变
C、向左平移
π
6
个单位长度，再把所得各点的横坐标缩短到原来的
1
2
倍，纵坐标不变
D、向左平移
π
6
个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变
如图是函数y=Asin（ωx+φ）的图象的一段，它的解析式为（　　）
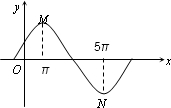精英家教网如图是函数y=Asin（ωx+φ）(A＞0，ω＞0，|φ|＜
π
2
)在一个周期内的图象，M、N分别是最大、最小值点，且
OM
⊥
ON
，则A•ω的值为（　　）
A、
π
6
B、
2
π
6
C、
5
π
4
D、
7
π
12
如图是函数y=Asin（ωx+φ）(A＞0，ω＞0，|φ|＜
π
2
)在一个周期内的图象，M、N分别是其最高点、最低点，MC⊥x轴，且矩形MBNC的面积为
7
π
12
，则A•ω的值为（　　）
如图是函数y=Asin（ωx+?）（x∈R，A＞0，ω＞0，0＜?＜
π
2
）在区间[-
π
6
，
5π
6
]上的图象，为了得到这个函数的图象，只需将y=sinx（x∈R）的图象上的所有的点（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网