题目内容
求函数在给定闭区间上的最值(或值域).(1)y=x+![]() ,x∈[0.01,100];
,x∈[0.01,100];
(2)y=sin2x-x,x∈[-![]() ,
,![]() ].注:(sin2x)′=2cos2x〕
].注:(sin2x)′=2cos2x〕
解:(1)令y′=(x+![]() )′=1-
)′=1-![]() =(1+x)(1-x)x2=0,
=(1+x)(1-x)x2=0,
解得x1=-1(舍去),x2=1.
当x=0.01时,y=0.01+![]() =100.01;
=100.01;
当x=1时,y=1+![]() =2;?
=2;?
当x=100时,y=100+![]() =100.01.
=100.01.
∴最大值为100.01,最小值是2.?
(2)令y′=(sin2x-x)′=2cos2x-1=0.?
∵x∈[-![]() ,
,![]() ],?
],?
∴解得x1=-![]() ,x2=
,x2=![]() .?
.?
当x=-![]() 时,y=sin(-π)+
时,y=sin(-π)+![]() =
=![]() ;?
;?
当x=-![]() 时,y=sin(-
时,y=sin(-![]() )+
)+![]() =-
=-![]() +
+![]() ;
;
当x=![]() 时,y=sin(
时,y=sin(![]() )-
)-![]() =
=![]() -
-![]() ;?
;?
当x=![]() ,y=sin(π)-
,y=sin(π)-![]() =-
=-![]() .?
.?
∵![]() >
>![]() -
-![]() >-
>-![]() +
+![]() >-
>-![]() ;?
;?
∴最大值是π2,最小值是-![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
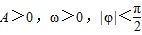 ,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2).
,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2).