题目内容
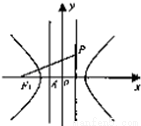
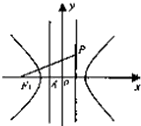 如图,F1是双曲线
如图,F1是双曲线 的左焦点,A是左准线与x轴的交点,若在右准线上存在一点P,使线段PF1的中垂线过点A,则双曲线的离心率的取值范围是________.
的左焦点,A是左准线与x轴的交点,若在右准线上存在一点P,使线段PF1的中垂线过点A,则双曲线的离心率的取值范围是________.

分析:设B是右准线与x轴的交点,先将几何条件“线段PF1的中垂线过点A”,转化为几何条件“|AF1|=|AP|”,再利用几何条件“|AP|≥|AB|”的不等关系|AF1|≥|AB|,最后将不等关系翻译为离心率不等式即可解得离心率的取值范围
解答:设B是右准线与x轴的交点
∵线段PF1的中垂线过点A,∴|AF1|=|AP|≥|AB|
∵|AF1|=c-
 ,|AB|=
,|AB|=
∴c-
 ≥
≥ ,即 c2≥3a2,e2≥3,e≥
,即 c2≥3a2,e2≥3,e≥
∴双曲线的离心率的取值范围是[
 ,+∞)
,+∞)故答案为

点评:本题考察了双曲线的定义和几何性质,双曲线准线的意义和离心率的范围的求法,找到恰当的不等关系是解决本题的关键

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
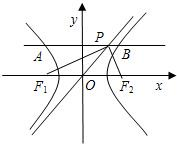 我们定义双曲线C:
我们定义双曲线C: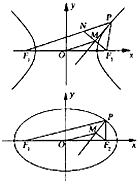 如图,P是双曲线
如图,P是双曲线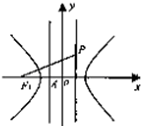 (2010•九江二模)如图,F1是双曲线
(2010•九江二模)如图,F1是双曲线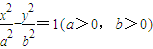 的左焦点,A是左准线与x轴的交点,若在右准线上存在一点P,使线段PF1的中垂线过点A,则双曲线的离心率的取值范围是 .
的左焦点,A是左准线与x轴的交点,若在右准线上存在一点P,使线段PF1的中垂线过点A,则双曲线的离心率的取值范围是 .