题目内容

在数列{an}中，a1=14,an+1=an-(n∈N*),则使an·an+1＜0成立的n的值是______________.

21

解析：由an+1=an-,得an+1-an=-,

∴数列{an}是首项为14，公差为-的等差数列.

∴an=14+(n-1)·(-)

=14-(n-1).

∴an·an+2=［14-(n-1)］［14-(n+1)］＜0.

∵d=-＜0,数列{an}单调递减,

∴

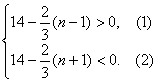
由①得n＜22,由②得n＞20,∴20＜n＜22.又n∈N*,故n=21.


练习册系列答案
相关题目
在数列{an}中，
a
 
1
=1，an=
1
2
an-1+1（n≥2），则数列{an}的通项公式为an=
2-21-n
2-21-n
．
在数列{an}中，a 1=
1
3
，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=
1
an
（n∈N*）．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{
an
n
}的前n项和为Tn，证明：
1
3
≤Tn＜
3
4
．
在数列{an}中，a=
12
，前n项和Sn=n2an，求an+1．
在数列{an}中,a1=a,前n项和Sn构成公比为q的等比数列,________________.

(先在横线上填上一个结论,然后再解答)

在数列{an}中，a，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=（n∈N*）．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{}的前n项和为Tn，证明：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网