Question

【题目】已知定义域为的函数是奇函数.

（1）求的值；

（2）判断函数的单调性，并用定义证明；

（3）当时，恒成立，求实数的取值范围.

Answer 1

【答案】（1） ，;（2）证明见解析；（3） ．

【解析】

试题分析：（1）寻找关于a,b的两个方程如（2）根据的单调性定义证明.（3）由单调递减则且满足的定义域，将问题转化为关于参数a的不等式.

试题解析：（1）∵在定义域为是奇函数.所以，即，∴.

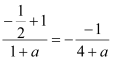又由，即，∴，检验知，当，时，原函数是奇函数.

（2）由（1）知，任取，设，则

，因为函数在上是增函数，且，所以，又，∴即，∴函数在上是减函数.

（3）因是奇函数，从而不等式等价于，因在上是减函数，由上式推得，即对一切有：恒成立，

设，令，则有，∴，∴，即的取值范围为.