题目内容
 .
.
- A.[2+∞)
- B.[-
 ,2)
,2) - C.(-∞,-
 ]
] - D.(-3,-
 ]
]
C
分析:由真数大于0求出原函数的定义域,因为外层函数对数函数是减函数,在定义域内求出内层函数的减区间,由复合函数的单调性可得原函数的增区间.
解答:令t=x2+x+6.则函数 化为
化为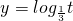 .
.
由x2+x+6>0,因为△=12-4×1×6=-230的解集为(-∞,+∞).
即函数 的定义域为R.
的定义域为R.
函数t=x2+x+6的减区间为(-∞,- ],而外层函数
],而外层函数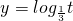 为减函数,
为减函数,
所以函数 的增区间为(-∞,-
的增区间为(-∞,- ].
].
故选C.
点评:本题考查复合函数的单调性,复合的两个函数同增则增,同减则减,一增一减则减,注意对数函数的定义域是求解的前提,考查学生发现问题解决问题的能力,是基础题.
分析:由真数大于0求出原函数的定义域,因为外层函数对数函数是减函数,在定义域内求出内层函数的减区间,由复合函数的单调性可得原函数的增区间.
解答:令t=x2+x+6.则函数
 化为
化为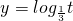 .
.由x2+x+6>0,因为△=12-4×1×6=-230的解集为(-∞,+∞).
即函数
 的定义域为R.
的定义域为R.函数t=x2+x+6的减区间为(-∞,-
 ],而外层函数
],而外层函数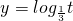 为减函数,
为减函数,所以函数
 的增区间为(-∞,-
的增区间为(-∞,- ].
].故选C.
点评:本题考查复合函数的单调性,复合的两个函数同增则增,同减则减,一增一减则减,注意对数函数的定义域是求解的前提,考查学生发现问题解决问题的能力,是基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 输入a=ln0.8,b=e
输入a=ln0.8,b=e| 1 |
| 2 |
| A、a=2-e,b=ln0.8 | ||
| B、a=ln0.8,b=2-e | ||
C、a=e
| ||
D、a=e
|