题目内容
已知集合A={x|-1≤x≤0},集合B={x|ax+b•2x-1<0,0≤a≤2,1≤b≤3}.若a,b∈N,则A∩B≠∅的概率为分析:(1)根据题意,分析a、b可得(a,b)的情况,令函数f(x)=ax+b•2x-1,x∈[-1,0],求导分析单调性可得其最小值,要使A∩B≠∅,只须-a+
-1<0,分析可得(a,b)能取的情况数,进而由几何概型的意义可得答案;
(2)因为a∈[0,2],b∈[1,3],确定其表示的平面区域,由(Ⅰ)可知A∩B=∅的(a,b)对应的关系式,借助线性规划分析,可得其区域,进而由几何概型的意义计算可得答案.
| b |
| 2 |
(2)因为a∈[0,2],b∈[1,3],确定其表示的平面区域,由(Ⅰ)可知A∩B=∅的(a,b)对应的关系式,借助线性规划分析,可得其区域,进而由几何概型的意义计算可得答案.
解答: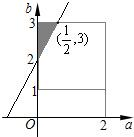 解:(1)因为a,b∈N,且0≤a≤2,1≤b≤3,
解:(1)因为a,b∈N,且0≤a≤2,1≤b≤3,
(a,b)可取(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),
(2,1),(2,2),(2,3)共9组.
令函数f(x)=ax+b•2x-1,x∈[-1,0],则f′(x)=a+bln2•2x.
因为a∈[0,2],b∈[1,3],所以f'(x)>0,即f(x)在[-1,0]上是单调增函数.
f(x)在[-1,0]上的最小值为-a+
-1.
要使A∩B≠∅,只须-a+
-1<0,即2a-b+2>0.
所以(a,b)只能取(0,1),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)7组.
所以A∩B≠∅的概率为
.
(2)因为a∈[0,2],b∈[1,3],
所以(a,b)对应的区域边长为2的,
正方形(如图),面积为4.
由(Ⅰ)可知,要使A∩B=∅,只须f(x)min=-a+
-1≥0?2a-b+2≤0,
所以满足A∩B=∅的(a,b)对应的区域是如图阴影部分.
所以S阴影=
×1×
=
.
所以A∩B=∅的概率为P=
=
.
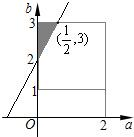 解:(1)因为a,b∈N,且0≤a≤2,1≤b≤3,
解:(1)因为a,b∈N,且0≤a≤2,1≤b≤3,(a,b)可取(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),
(2,1),(2,2),(2,3)共9组.
令函数f(x)=ax+b•2x-1,x∈[-1,0],则f′(x)=a+bln2•2x.
因为a∈[0,2],b∈[1,3],所以f'(x)>0,即f(x)在[-1,0]上是单调增函数.
f(x)在[-1,0]上的最小值为-a+
| b |
| 2 |
要使A∩B≠∅,只须-a+
| b |
| 2 |
所以(a,b)只能取(0,1),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)7组.
所以A∩B≠∅的概率为
| 7 |
| 9 |
(2)因为a∈[0,2],b∈[1,3],
所以(a,b)对应的区域边长为2的,
正方形(如图),面积为4.
由(Ⅰ)可知,要使A∩B=∅,只须f(x)min=-a+
| b |
| 2 |
所以满足A∩B=∅的(a,b)对应的区域是如图阴影部分.
所以S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
所以A∩B=∅的概率为P=
| ||
| 4 |
| 1 |
| 16 |
点评:本题重点考查几何概型的意义与几何概型的计算,解题时注意(1)(2)中a、b的范围不同,因而采取不同的分析、计算方法.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目