题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() 。斜率为1的直线
。斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以
两点,以![]() 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的面积。
的面积。
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据椭圆的简单几何性质知![]() ,又
,又![]() ,写出椭圆的方程;(2)先斜截式设出直线
,写出椭圆的方程;(2)先斜截式设出直线![]() ,联立方程组,根据直线与圆锥曲线的位置关系,可得出
,联立方程组,根据直线与圆锥曲线的位置关系,可得出![]() 中点为
中点为![]() 的坐标,再根据△
的坐标,再根据△![]() 为等腰三角形知
为等腰三角形知![]() ,从而得
,从而得![]() 的斜率为
的斜率为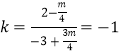 ,求出
,求出![]() ,写出
,写出![]() :
:![]() ,并计算
,并计算![]() ,再根据点到直线距离公式求高,即可计算出面积.
,再根据点到直线距离公式求高,即可计算出面积.
试题解析:(1)由已知得![]() ,
,![]() ,解得
,解得![]() ,又
,又![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
由 得
得![]() ①
①
设![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() (
(![]() ),
),![]() 中点为
中点为![]() ,
,
则![]() ,
,![]() ,
,
因为![]() 是等腰△
是等腰△![]() 的底边,所以
的底边,所以![]() .
.
所以![]() 的斜率为
的斜率为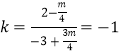 ,解得
,解得![]() ,此时方程①为
,此时方程①为![]() .
.
解得![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,
此时,点![]() 到直线
到直线![]() :
:![]() 的距离
的距离![]() ,
,
所以△![]() 的面积
的面积![]() .
.

练习册系列答案
相关题目
【题目】已知表1是某年部分日期的天安门广场升旗时刻表.
表1:某年部分日期的天安门广场升旗时刻表

将表1中的升旗时刻化为分数后作为样本数据(如:![]() 可化为
可化为![]() ).
).
(Ⅰ)请补充完成下面的频率分布表及频率分布直方图;
|
|
(Ⅱ)若甲学校从上表日期中随机选择一天观看升旗.试估计甲学校观看升旗的时刻早于6:00的概率;
(Ⅲ)若甲,乙两个学校各自从表1中五月、六月的日期中随机选择一天观看升旗, 求两校观看升旗的时刻均不早于5:00的概率.



