题目内容
16.已知直线m,n与平面α,β,下列命题中错误的是( )| A. | 若m⊥α,n⊥α,则m∥n | B. | 若m⊥β,n∥β,则m⊥n | ||
| C. | 若m⊥α,n⊥β,α⊥β,则m⊥n | D. | 若m∥n,n?α,则m∥α |
分析 根据空间线面位置关系的性质和判定进行逐项分析或证明.
解答 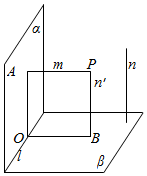 解:对于A,由于垂直于同一个平面的两条直线平行,故A正确;
解:对于A,由于垂直于同一个平面的两条直线平行,故A正确;
对于B,∵n∥β,∴平面β内存在直线b∥n,
∵m⊥β,b?β,∴m⊥b
又b∥n,∴m⊥n.故B正确.
对于C,在直线m上取点P,过P作n的平行线n′,则n′⊥β.
假设m∩α=A,n′∩β=B,α∩β=l,过A作AO⊥l于O,连结OB.
∵α∩β=l,α⊥β,AO⊥l,AO?α,
∴AO⊥β,又n′⊥β,
∴AO∥n′,同理BO∥m,
∴四边形AOBP是平行四边形,
又m⊥α,AO?α,
∴PA⊥AO,
∴四边形AOBP是矩形,
∴m⊥n′,又n∥n′,
∴m⊥n.故C正确.
对于D,当m?α时,显然结论不成立.故D错误.
故选:D.
点评 本题考查了空间线面位置关系的判定与性质,属于中档题.

练习册系列答案
相关题目
7.已知集合A={x|x(1-x)>0},B={0,1,2},则A∩B=( )
| A. | ∅ | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
4.已知A,B为圆C:(x-a)2+(y-b)2=9(a,b∈R)上的两个不同的点,且满足|$\overrightarrow{CA}$+$\overrightarrow{CB}$|=2$\sqrt{2}$,则|$\overrightarrow{AB}$|=( )
| A. | 1 | B. | $\sqrt{7}$ | C. | 2 | D. | 2$\sqrt{7}$ |
11.如果实数x,y满足条件$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-y+2≥0}\\{x-a≤0}\end{array}\right.$,若z=$\frac{y-1}{x+1}$的最小值小于$\frac{1}{2}$,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | ($\frac{1}{5}$,1) | D. | ($\frac{1}{5}$,+∞) |
1.已知M为△ABC内一点,$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$,则△ABM和△ABC的面积之比为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
8.若非空集合A={x|a+1≤x≤3a-5},集合B={x|1≤x≤16},则满足A⊆(A∩B)的实数a的取值范围是( )
| A. | [0,7] | B. | [7,15] | C. | [3,7] | D. | [3,15] |
6.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F1,P为左支上一点,|PF1|=a,P0与P关于原点对称,且$\overrightarrow{{P}_{0}{F}_{1}}$$•\overrightarrow{P{F}_{1}}$=0.则双曲线的渐近线方程为( )
| A. | y=±x | B. | y=$±\frac{\sqrt{6}}{2}$x | C. | y=$±\frac{\sqrt{3}}{2}$x | D. | y=±2x |