题目内容
若向量|a|=|b|=1，且a+b=（1，0），求a与b的坐标.解法1：设a=（m，n），b=（p，q），则有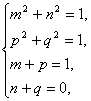
解得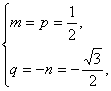
或
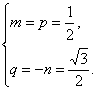
故所求向量为a=（
，
），b=（
，-
），或a=（
，-
），b=（
，
）.
解法2：设a=（cosα，sinα），b=（cosβ，sinβ），
则有
由①②得（1-cosβ）2+sin2β=1，即cosβ=
.
将cosβ=
代入①得
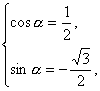
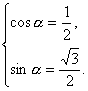
故所求向量为a=（
，
），b=（
，-
），或a=（
，-
），b=（
，
）
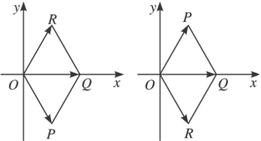
解法3：设a=
=P（m，n），b=
=R（p，q），
=Q（1，0）.
由题意有
.
则四边形OPQR为平行四边形.
又∵|
|=|
|=|
|=1，
∴△OPQ，△OQR均为正三角形，故所求向量为
a=（
，
），b=（
，-
），或a=（
，-
），b=（
，
）.
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目