题目内容
从1,2,3,4,5,6中任取3个数字组成无重复数字的三位数,其中若同时含有1和3时,3必须放在1的前面,若含有1或3其中之一时,则应该将其排在其他数字的前面,这样的不同三位数的个数为 个.
考点:排列、组合及简单计数问题
专题:排列组合
分析:同时含有1和3时,1和3的顺序只有两种,所求的结果除以2即可,有含有1或3其中之一时,只要选2和数排在后面即可,根据分类计数原理可得.
解答:
解:由题意分两类
第一类,同时含有1和3时,3必须放在1的前面有
•
=12个,
第二类,含有1或3其中之一时,则应该将其排在其他数字的前面
•
=48个,
根据分类计数原理可得,这样的不同三位数的个数为12+48=60个.
故答案为:60.
第一类,同时含有1和3时,3必须放在1的前面有
| 1 |
| 2 |
| ×C | 1 4 |
| A | 3 3 |
第二类,含有1或3其中之一时,则应该将其排在其他数字的前面
| A | 1 2 |
| A | 2 4 |
根据分类计数原理可得,这样的不同三位数的个数为12+48=60个.
故答案为:60.
点评:本题考查了分类计数原理,注意排列的顺序性,属于中档题.

练习册系列答案
相关题目
(理科)
tan21°tan39°-tan159°+tan39°=( )
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
在数列{an}中,a1=5,an+1=(1+
)an,则( )
| 1 |
| n |
| A、an=3n+2 |
| B、an=6n-1 |
| C、an=5n |
| D、an=4n+1 |
计算2sin15°•cos30°+sin15°等于( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
由①y=2x+5是一次函数;②y=2x+5的图象是一条直线;③一次函数的图象是一条直线.写一个“三段论”形式的正确推理,则作为大前提、小前提和结论的分别是( )
| A、②①③ | B、③①② |
| C、①②③ | D、②③① |
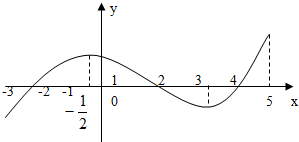 如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数的图象如图所示,给出下列判断: