题目内容
(本题满分14分)
已知数列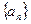 中,
中,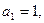 且点
且点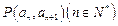 在直线
在直线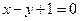 上.
上.
(1)求数列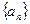 的通项公式;
的通项公式;
(2)若函数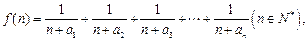 求函数
求函数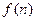 的最小值;
的最小值;
(3)设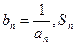 表示数列
表示数列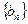 的前
的前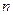 项和,
项和,
试证明: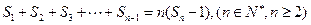 .
.
已知数列
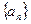 中,
中,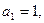 且点
且点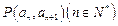 在直线
在直线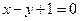 上.
上.(1)求数列
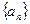 的通项公式;
的通项公式;(2)若函数
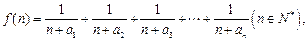 求函数
求函数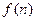 的最小值;
的最小值;(3)设
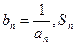 表示数列
表示数列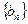 的前
的前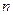 项和,
项和,试证明:
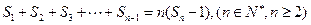 .
.(1)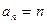 (2)
(2)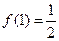
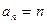 (2)
(2)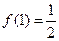
解 :(1)由点P
:(1)由点P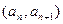 在直线
在直线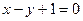 上,即
上,即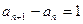 , …2分
, …2分
且 ,数列{
,数列{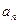 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列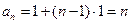 ,
,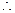
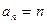 ……………4分
……………4分
(2)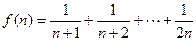
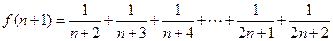 …………………6分
…………………6分
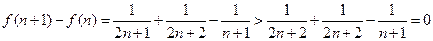
所以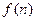 是单调递增,故
是单调递增,故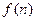 的最小值是
的最小值是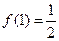 ……………10分
……………10分
 (3)
(3)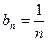 ,可得
,可得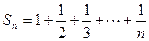 ,
,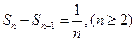 ……………11分
……………11分
 ……………12分
……………12分
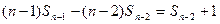
…………
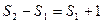
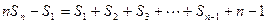
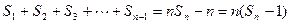 ,
,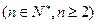 ……………14分
……………14分
另解: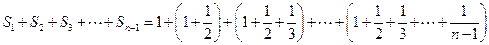
此式中有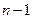 个1,有
个1,有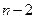 个
个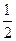 ,
, ,1个
,1个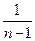 。 ………………12分
。 ………………12分
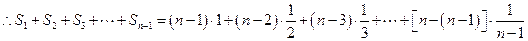
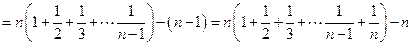
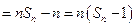 。
。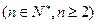 ………………14分
………………14分
 :(1)由点P
:(1)由点P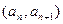 在直线
在直线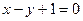 上,即
上,即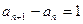 , …2分
, …2分且
 ,数列{
,数列{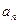 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列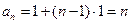 ,
,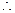
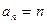 ……………4分
……………4分(2)
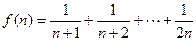
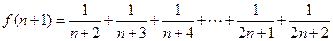 …………………6分
…………………6分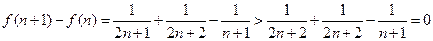
所以
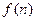 是单调递增,故
是单调递增,故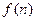 的最小值是
的最小值是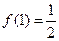 ……………10分
……………10分 (3)
(3)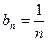 ,可得
,可得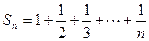 ,
,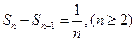 ……………11分
……………11分 ……………12分
……………12分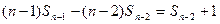
…………
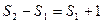
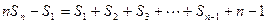
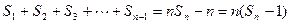 ,
,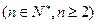 ……………14分
……………14分另解:
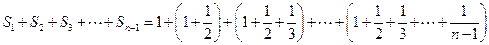
此式中有
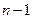 个1,有
个1,有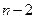 个
个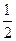 ,
, ,1个
,1个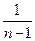 。 ………………12分
。 ………………12分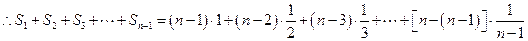
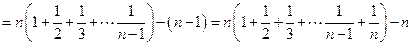
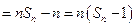 。
。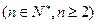 ………………14分
………………14分
练习册系列答案
相关题目
 容影响了市容市貌. 今年该市决定引进一
容影响了市容市貌. 今年该市决定引进一 种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是
种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是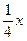 ,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经
,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经 过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满
过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满 足洗车净水需求)
足洗车净水需求)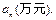
 与n的关系式;
与n的关系式;
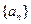 的首项
的首项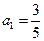 ,
,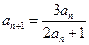 ,
,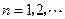 .
.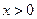 ,
,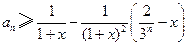 ,
,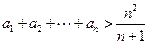 .
.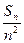 ,如果存在正整数M,使得对一切正整数n,Tn≤M都成立.则M的最小值是__________.
,如果存在正整数M,使得对一切正整数n,Tn≤M都成立.则M的最小值是__________.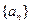 的前
的前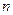 项和为
项和为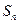 ,若
,若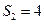 ,
,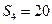 ,则该数列的公差
,则该数列的公差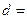 ( )
( )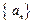 中,
中, ,
, ,则
,则 等于C
等于C