题目内容
 已知:在空间四边形DABC中,DA⊥BC,DB⊥AC.用两种方法证明:DC⊥AB.
已知:在空间四边形DABC中,DA⊥BC,DB⊥AC.用两种方法证明:DC⊥AB.
 证明:法一:
证明:法一: =
=
=

=

故DC和AB互相垂直.
法二:证明:取AB中点E,连接DE、CE,∵BC=AC,E为AB中点,∴CE⊥AB,
同理DE⊥AB.
∵CE∩DE=E,
∴AB⊥平面CDE,
∴AB⊥CD.
分析:法一:将
 用
用 ,
,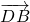 来表示;
来表示;  用
用 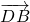 ,
, 表示;利用向量的运算律及向量垂直的数量积为0求出
表示;利用向量的运算律及向量垂直的数量积为0求出  ;判断出垂直.
;判断出垂直.法二:取AB中点E,由等腰三角形的性质可得CE⊥AB,且DE⊥AB,再由线面垂直的判定定理可得AB⊥平面CDE,从而得到AB⊥CD.
点评:本题考查向量垂直的充要条件、向量的运算法则、向量的运算律利用想向量垂直判断线垂直.本题还考查证明线线垂直、线面垂直的方法,直线与平面垂直的判定、性质的应用,取取AB中点E,是解题的突破口.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
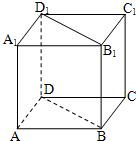 已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是( )
已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是( )| A、两两异面 | B、两两平行 | C、交于一点 | D、两两相交 |
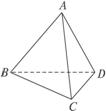
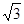 ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD=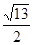 ,AC=
,AC=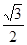 , AC和BD所成的角是( )
, AC和BD所成的角是( )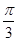 B.
B.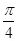 C.
C.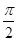 D.
D.