题目内容
已知下列四个函数:
(1)f(x)=lgx2,g(x)=2lgx;
(2)(2)f(x)=x-1,g(x)=
;
(3)f(x)=log22x,g(x)=
;
(4)f(x)=
,g(x)=f-1(x).
则表示同一函数的是:
(1)f(x)=lgx2,g(x)=2lgx;
(2)(2)f(x)=x-1,g(x)=
| x2-2x+1 |
(3)f(x)=log22x,g(x)=
| 3 | x3 |
(4)f(x)=
| 1 |
| x |
则表示同一函数的是:
(3)(4)
(3)(4)
.分析:逐一检验各个选项中的两个函数是否具有相同的定义域、值域、对应关系,只有这三者完全相同时,两个函数才是同一个函数.
解答:解:(1)f(x)=lgx2,函数的定义域为{x|x≠0},g(x)=2lgx的函数的定义域{x|x>0},不是同一个函数.
(2)中的函数g(x)=
=|x-1|,解析式不同,不是同一函数;
(3)f(x)=log22x=x,g(x)=
=x;定义域、值域、对应关系均相同,是同一函数;
(4)中的函数g(x)=f-1(x)=
与f(x)=
定义域、值域、对应关系均相同,是同一函数.
即表示同一函数的是:(3),(4).
答案为:(3),(4).
(2)中的函数g(x)=
| x2-2x+1 |
(3)f(x)=log22x=x,g(x)=
| 3 | x3 |
(4)中的函数g(x)=f-1(x)=
| 1 |
| x |
| 1 |
| x |
即表示同一函数的是:(3),(4).
答案为:(3),(4).
点评:本题考查函数的三要素:定义域、值域、对应关系.两个函数只有当定义域、值域、对应关系完全相同时,才是同一个函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ;
;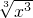 ;
; ,g(x)=f-1(x).
,g(x)=f-1(x). ;
; ;
; ,g(x)=f-1(x).
,g(x)=f-1(x).