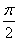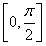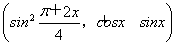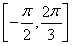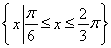题目内容
已知函数f(x)=2 ·sin
·sin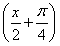 cos
cos -sin(x+π).
-sin(x+π).
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
(1)2π(2)最大值2,最小值-1
【解析】(1)因为f(x)= sin
sin +sinx=
+sinx= cosx+sinx=2
cosx+sinx=2 =2sin
=2sin ,所以f(x)的最小正周期为2π.
,所以f(x)的最小正周期为2π.
(2)∵将f(x)的图象向右平移 个单位,得到函数g(x)的图象,∴g(x)=f
个单位,得到函数g(x)的图象,∴g(x)=f =2sin
=2sin =2sin
=2sin .∵x∈[0,π],∴x+
.∵x∈[0,π],∴x+ ∈
∈ ,
,
∴当x+ =
= ,即x=
,即x= 时,sin
时,sin =1,g(x)取得最大值2.
=1,g(x)取得最大值2.
当x+ =
= ,即x=π时,sin
,即x=π时,sin =-
=- ,g(x)取得最小值-1.
,g(x)取得最小值-1.

练习册系列答案
相关题目