Question

【题目】已知，且．设函数在区间内单调递减； 曲线与轴交于不同的两点，如果“”为真命题，“”为假命题，求实数的取值范围．

Answer 1

【答案】）∵且,

∴命题P为真

命题Q为真

或

∵“”为真，“”为假

∴命题一个为真一个为假

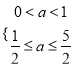∴或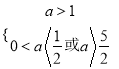

∴实数的取值范围是.

【解析】试题分析：本题考查复合命题真假判定，考查了指数函数的单调性与曲线的交点问题。根据指数函数在区间内单调递减，可得；曲线与轴交于不同的两点，则，求出或。因为“”为真命题，“”为假命题，所以与恰好一真一假，即可求出实数的取值范围。

试题解析：由“函数在区间内单调递减”

可知，

由“曲线与轴交于不同的两点”

可知或，

因为“”为真命题，“”为假命题，

所以与恰好一真一假，

当真， 假时， ，

即.

当假， 真时， ，

即.

综上可知， 的取值范围为： .