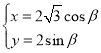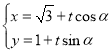题目内容
【题目】在平面直角坐标系![]() 内,有一动点
内,有一动点![]() 到直线
到直线![]() 的距离和到点
的距离和到点![]() 的距离比值是
的距离比值是![]()
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() (异于点
(异于点![]() )为曲线
)为曲线![]() 上一个动点,过点
上一个动点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交曲线
交曲线![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)直接根据题意设点,列式,化简,即可求出动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)先考虑特殊情况,当直线![]() 的斜率为
的斜率为![]() 时,可计算出
时,可计算出![]() ,再考虑一般情况,
,再考虑一般情况,
当直线![]() 的斜率不为
的斜率不为![]() 时,设直线
时,设直线![]() 的方程为
的方程为![]() ,与椭圆
,与椭圆![]() 的方程联立求出点
的方程联立求出点![]() 的坐标得出
的坐标得出![]() 的长,同理,将直线
的长,同理,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立求出
的方程联立求出![]() ,继而得到
,继而得到![]() 的表达式,最后根据函数知识即可求出
的表达式,最后根据函数知识即可求出![]() 的最小值.
的最小值.
(1)设动点![]() 的坐标为
的坐标为![]() ,根据题意得
,根据题意得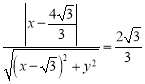 ,再考虑一般情况,当
,再考虑一般情况,当
化简得曲线![]() 的方程为:
的方程为:![]() .
.
(2)当直线![]() 的斜率为
的斜率为![]() 时,
时,![]() 为椭圆
为椭圆![]() 的短轴,则
的短轴,则![]() .
.
所以![]()
当直线![]() 的斜率不为
的斜率不为![]() 时,设直线
时,设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
由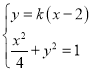 得
得![]() .
.
设![]() 所以
所以![]() ,
,![]()
故![]() ,得
,得![]()
设![]() ,由椭圆对称性可知
,由椭圆对称性可知![]() .
.
由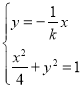 解得
解得![]()
![]() ,所以
,所以![]()
所以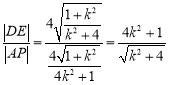
设![]() ,则
,则![]()
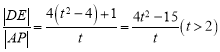 ,令
,令![]() ,则
,则![]()
所以![]() 是一个增函数,所以
是一个增函数,所以![]()
综上,![]() 的最小值是
的最小值是![]() .
.

练习册系列答案
相关题目