题目内容
已知m>0,f(x)是定义在R上周期为4的函数,在x∈(-1,3]上f(x)=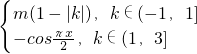 ,若方程f(x)=
,若方程f(x)= 恰有5个实数解,则m的取值范围是
恰有5个实数解,则m的取值范围是
- A.(
 ,
, )
) - B.[
 ,
, ]
] - C.[
 ,+∞]
,+∞] - D.(
 ,+∞)
,+∞)
A
分析:将方程f(x)= 恰有5个实数解,转化为一个函数y=f(x)的图象与直线y=
恰有5个实数解,转化为一个函数y=f(x)的图象与直线y= 的位置关系研究即可得出答案.
的位置关系研究即可得出答案.
解答: 解:方程f(x)=
解:方程f(x)= ,
,
令 y=f(x)= ,y=
,y= ,
,
分别画出它们的图象,如图,其中A(4,m),B(8,m).由图可知,
若方程f(x)= 恰有5个实数解,
恰有5个实数解,
则点A必须在直线y= 的上方,点B在直线y=
的上方,点B在直线y= 的下方,即
的下方,即 ,
,
∴m∈( ,
, )
)
则m的取值范围是( ,
, ).
).
故选A.
点评:本题主要考查根的存在性及根的个数判断,解答关键是利用直线与曲线的位置关系,要注意数形结合及转化思想的应用.
分析:将方程f(x)=
 恰有5个实数解,转化为一个函数y=f(x)的图象与直线y=
恰有5个实数解,转化为一个函数y=f(x)的图象与直线y= 的位置关系研究即可得出答案.
的位置关系研究即可得出答案.解答:
 解:方程f(x)=
解:方程f(x)= ,
,令 y=f(x)=
 ,y=
,y= ,
,分别画出它们的图象,如图,其中A(4,m),B(8,m).由图可知,
若方程f(x)=
 恰有5个实数解,
恰有5个实数解,则点A必须在直线y=
 的上方,点B在直线y=
的上方,点B在直线y= 的下方,即
的下方,即 ,
,∴m∈(
 ,
, )
)则m的取值范围是(
 ,
, ).
).故选A.
点评:本题主要考查根的存在性及根的个数判断,解答关键是利用直线与曲线的位置关系,要注意数形结合及转化思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知m<0,f(x)=mx3+
,且f′(1)≥-18,则实数m等于( )
| 27x |
| m |
| A、-9 | B、-3 | C、3 | D、9 |
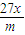 ,且f′(1)≥-18,则实数m等于( )
,且f′(1)≥-18,则实数m等于( )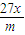 ,且f′(1)≥-18,则实数m等于( )
,且f′(1)≥-18,则实数m等于( )