题目内容
已知f(x)=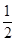 x2-cos x,x∈[-1,1],则导函数f′(x)是( )
x2-cos x,x∈[-1,1],则导函数f′(x)是( )
| A.仅有最小值的奇函数 |
| B.既有最大值,又有最小值的偶函数 |
| C.仅有最大值的偶函数 |
| D.既有最大值,又有最小值的奇函数 |
D
解析试题分析: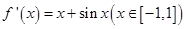 ,
, ,故
,故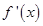 为奇函数.
为奇函数.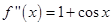 ,在
,在 时
时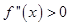 ,所以
,所以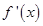 在
在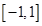 为增函数,则函数既有最大值,又有最小值.
为增函数,则函数既有最大值,又有最小值.
考点:函数的奇偶性,导数与函数单调性的关系.

练习册系列答案
相关题目
已知函数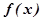 =
= ,
,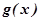 =
=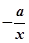 ,若至少存在一个
,若至少存在一个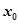 ∈[1,e],使
∈[1,e],使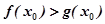 成立,则实数a的范围为( ).
成立,则实数a的范围为( ).
| A.[1,+∞) | B.(0,+∞) | C.[0,+∞) | D.(1,+∞) |
已知函数 ,若曲线
,若曲线 存在与直线
存在与直线 平行的切线,则实数
平行的切线,则实数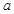 的取值范围是( )
的取值范围是( )
A.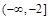 | B. | C.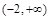 | D.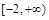 |
在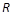 上可导的函数
上可导的函数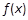 的图形如图所示,
的图形如图所示,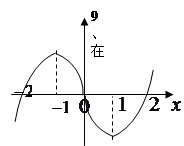 则关于
则关于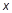 的不等式
的不等式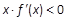 的解集为( ).
的解集为( ).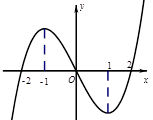
A.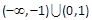 | B.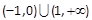 |
C.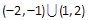 | D. |
函数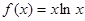 ,则( )
,则( )
A.在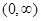 上递增; 上递增; | B.在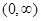 上递减; 上递减; |
C.在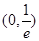 上递增; 上递增; | D.在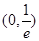 上递减 上递减 |
若函数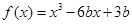 在(0,1)内有极小值,则实数b的取值范围是( )
在(0,1)内有极小值,则实数b的取值范围是( )
| A.(0,1) | B.(0,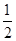 ) ) | C.(0,+∞) | D.(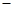 ∞,1) ∞,1) |
若函数f(x)=2x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
| A.[1,+∞) | B.[1,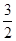 ) ) | C.[1,2) | D.[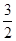 ,2) ,2) |
 的图象如图所示,若
的图象如图所示,若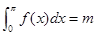 ,则
,则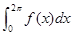 等于( )
等于( )
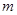 B.2m C.0 D.-m
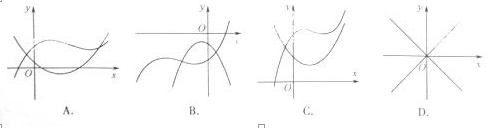
B.2m C.0 D.-m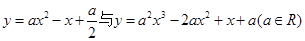 的图像不可能的是( )
的图像不可能的是( )