题目内容
在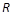 上可导的函数
上可导的函数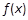 的图形如图所示,
的图形如图所示,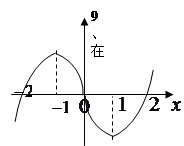 则关于
则关于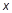 的不等式
的不等式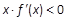 的解集为( ).
的解集为( ).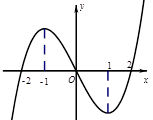
A.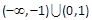 | B.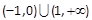 |
C.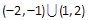 | D. |
A
解析试题分析:由图象可知f′(x)=0的解为x=-1和x=1
函数f(x)在(-∞,-1)上增,在(-1,1)上减,在(1,+∞)上增
∴f′(x)在(-∞,-1)上大于0,在(-1,1)小于0,在(1,+∞)大于0
当x<0时,f′(x)>0解得x∈(-∞,-1)
当x>0时,f′(x)<0解得x∈(0,1)
综上所述,x∈(-∞,-1)∪(0,1),故选A.
考点:函数的图象;导数的运算;其他不等式的解法.

练习册系列答案
相关题目
定义在R上的函数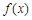 ,若对任意
,若对任意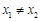 ,都有
,都有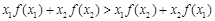 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:①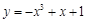 ;②
;② ;③
;③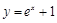 ;④
;④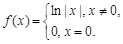 其中是“H函数”的个数为
其中是“H函数”的个数为
| A.1 | B.2 | C.3 | D.4 |
曲线 在(1,1)处的切线方程是( )
在(1,1)处的切线方程是( )
A.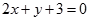 | B. |
C. | D. |
 等于( )
等于( )
A. | B.2 | C. | D. |
设 ,
, ,
, ,……,
,……, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
由直线 ,
, ,曲线
,曲线 及
及 轴所围成的图形的面积是( )
轴所围成的图形的面积是( )
A. | B. | C. | D. |
已知f(x)=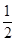 x2-cos x,x∈[-1,1],则导函数f′(x)是( )
x2-cos x,x∈[-1,1],则导函数f′(x)是( )
| A.仅有最小值的奇函数 |
| B.既有最大值,又有最小值的偶函数 |
| C.仅有最大值的偶函数 |
| D.既有最大值,又有最小值的奇函数 |
设函数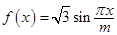 .若存在
.若存在 的极值点
的极值点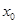 满足
满足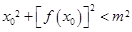 ,则m的取值范围是( )
,则m的取值范围是( )
A. | B.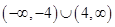 |
C.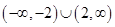 | D.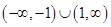 |
已知函数f(x)=1+x-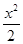 +
+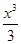 -
-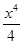 +…+
+…+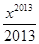 ,则下列结论正确的是( )
,则下列结论正确的是( )
| A.f(x)在(0,1)上恰有一个零点 |
| B.f(x)在(0,1)上恰有两个零点 |
| C.f(x)在(-1,0)上恰有一个零点 |
| D.f(x)在(-1,0)上恰有两个零点 |