题目内容
已知函数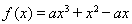 ,其中
,其中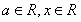 .
.
(1)当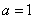 时,求函数
时,求函数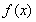 在
在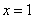 处的切线方程;
处的切线方程;
(2)若函数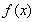 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求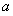 的取值范围;
的取值范围;
(3)已知 ,如果存在
,如果存在 ,使得函数
,使得函数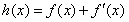
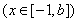 在
在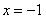 处取得最小值,试求
处取得最小值,试求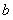 的最大值.
的最大值.
【答案】
(1) 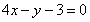 (2)
(2)  (3)
(3)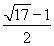
【解析】
试题分析:(1) 利用导数求切线方程,关键在于理解切点的三个含义,一是在切点处的导数值为切线的斜率,二是切点在曲线上,即切点坐标满足曲线方程,三是切点在直线上,即切点坐标满足直线方程,有时这一条件用直线两点间斜率公式表示.因为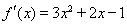 所以
所以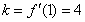 ,再根据点斜式写出切线方程. (2)利用导数研究函数单调性,往往转化为研究导函数为零时方程根的情况,本题函数
,再根据点斜式写出切线方程. (2)利用导数研究函数单调性,往往转化为研究导函数为零时方程根的情况,本题函数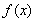 在区间(1,2)上不是单调函数,就转化为
在区间(1,2)上不是单调函数,就转化为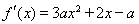 在区间(1,2)上有不相等的根,可由实根分布列充要条件,也可利用变量分离结合图象求函数对应区域范围,(3)已知函数最值求参数取值范围,可从恒成立角度出发,实现等价转化,也可分类讨论求最值列等式.本题采取
在区间(1,2)上有不相等的根,可由实根分布列充要条件,也可利用变量分离结合图象求函数对应区域范围,(3)已知函数最值求参数取值范围,可从恒成立角度出发,实现等价转化,也可分类讨论求最值列等式.本题采取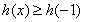 对
对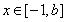 恒成立较好.转化为二次函数恒成立可从四个方面研究:一是开口方向,二是对称轴,三是判别式,四是区间端点函数值的正负.
恒成立较好.转化为二次函数恒成立可从四个方面研究:一是开口方向,二是对称轴,三是判别式,四是区间端点函数值的正负.
试题解析:(1)解:当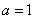 时,
时,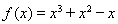 ,则
,则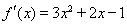 ,故
,故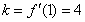 2分
2分
又切点为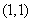 ,故所求切线方程为
,故所求切线方程为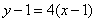 ,即
,即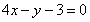 4分
4分
(2)由题意知,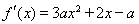 在区间(1,2)上有不重复的零点,
在区间(1,2)上有不重复的零点,
由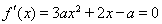 ,得
,得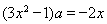 ,因为
,因为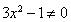 ,所以
,所以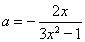 7分令
7分令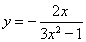 ,则
,则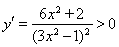 ,故
,故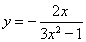 在区间(1,2)上是增函数,所以其值域为
在区间(1,2)上是增函数,所以其值域为 ,从而
,从而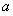 的取值范围是
的取值范围是 9分
9分
(3)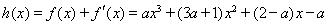 ,
,
由题意知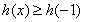 对
对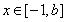 恒成立,即
恒成立,即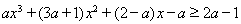 对
对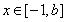 恒成立,即
恒成立,即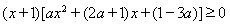 ①对
①对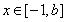 恒成立 11分
恒成立 11分
当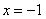 时,①式显然成立;
时,①式显然成立;
当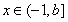 时,①式可化为
时,①式可化为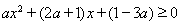 ②,
②,
令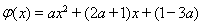 ,则其图象是开口向下的抛物线,所以
,则其图象是开口向下的抛物线,所以 13分
13分
即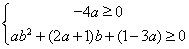 ,其等价于
,其等价于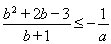 ③ ,
③ ,
因为③在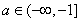 时有解,所以
时有解,所以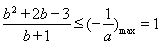 ,解得
,解得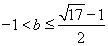 ,
,
从而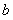 的最大值为
的最大值为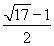 16分
16分
考点:利用导数求切线方程,利用导数研究函数单调性,不等式恒成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 其中常数
其中常数 .
. 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 时,若函数
时,若函数 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围; 在点
在点 处的切线方程为
处的切线方程为 当
当 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由. 其中常数
其中常数
 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 时,给出两类直线:
时,给出两类直线: 与
与 ,其中
,其中 为常数,判断这两类直线中是否存在
为常数,判断这两类直线中是否存在 的切线,若存在,求出相应的
的切线,若存在,求出相应的 或
或 的值,若不存在,说明理由.
的值,若不存在,说明理由. 上的函数
上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当 若
若 在
在 为函数
为函数 其中实数
其中实数 。
。 在点
在点 处的切线方程;
处的切线方程;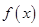 的单调性。
的单调性。