题目内容
正三棱锥V-ABC中,AB=1,侧棱VA,VB,VC两两互相垂直,则底面中心到侧面的距离为
- A.

- B.

- C.

- D.

C
分析:正三棱锥V-ABC中,AB=1,侧棱VA,VB,VC两两互相垂直,
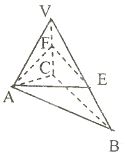
解答: 解:正三棱锥V-ABC中,AB=1,侧棱VA,VB,VC两两互相垂直,如图
解:正三棱锥V-ABC中,AB=1,侧棱VA,VB,VC两两互相垂直,如图
O是底面正三角形ABC的中心,O到侧面距离OP是VC的
因为AB=1所以VA=
所以OP=
故选C.
点评:本题考查棱锥的结构特征,考查空间想象能力,是中档题.
分析:正三棱锥V-ABC中,AB=1,侧棱VA,VB,VC两两互相垂直,
解答:
 解:正三棱锥V-ABC中,AB=1,侧棱VA,VB,VC两两互相垂直,如图
解:正三棱锥V-ABC中,AB=1,侧棱VA,VB,VC两两互相垂直,如图O是底面正三角形ABC的中心,O到侧面距离OP是VC的

因为AB=1所以VA=

所以OP=

故选C.
点评:本题考查棱锥的结构特征,考查空间想象能力,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
正三棱锥V-ABC中,AB=1,侧棱VA,VB,VC两两互相垂直,则底面中心到侧面的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,侧棱长为
如图所示,侧棱长为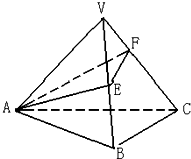 (文科)侧棱长为3
(文科)侧棱长为3