Question

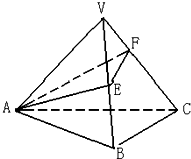（文科）侧棱长为3

3

的正三棱锥V-ABC中，∠AVB=∠BVC=∠CVA=40°，过点A作截面AEF，则截面AEF周长的最小值为

9

．

Answer 1

分析：沿着侧棱VA把正三棱锥V-ABC展开在一个平面内，如图，则AA′即为截面△AEF周长的最小值，且∠AVA′=3×40=120°．△VAA′中，由余弦定理可得 AA'的值．

解答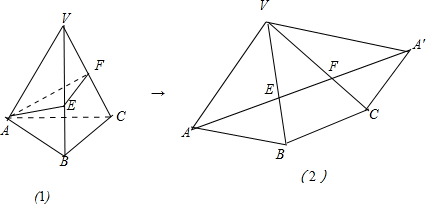：解：如图所示：沿着侧棱VA把正三棱锥V-ABC展开在一个平面内，如图（2），
则AA′即为截面△AEF周长的最小值，且∠AVA′=3×40=120°．
△VAA′中，由余弦定理，得
 AA'=

VA2+(VA‘)2-2VA•VA′sin∠AVA′

=

27+27-2×3 3 ×3 3×cos120°

=9．
故答案为：9．

点评：本题主要考查余弦定理的应用，棱锥的结构特征，利用棱锥的侧面展开图研究几条线段和的最小值问题，是一种重要的解题方法，属于基础题．