题目内容
(2011•温州一模)所有正奇数如下数表排列(表中下一行中的数的个数是上一行中数的个数的2倍)
第一行 1
第一行 3 5
第一行 7 9 11 13
…
则第6行中的第3个数是
第一行 1
第一行 3 5
第一行 7 9 11 13
…
则第6行中的第3个数是
67
67
.分析:根据题意,分析可得,数表中的数从上到下,每行从左到右依次一个首项为1,公差为2的等差数列,可得其通项,又由表中下一行中的数的个数是上一行中数的个数的2倍,且第1有1个数,可得则前5行的数的个数,进而可得第6行中的第3个数为这个数列的第34个数,由等差数列的通项公式可得答案.
解答:解:根据题意,分析数表可得,表中的数从上到下,每行从左到右依次为1、3、5、7、…;
是一个首项为1,公差为2的等差数列,设为{an},则其通项为an=2n-1;
而表中下一行中的数的个数是上一行中数的个数的2倍,且第1行有1个数,
则前5行有1+2+4+8+16=31个数,则第6行中的第3个数为这个数列的第34个数,
即{an}这个数列的第34项,易得an=2n-1=2×34-1=67;
故答案为67.
是一个首项为1,公差为2的等差数列,设为{an},则其通项为an=2n-1;
而表中下一行中的数的个数是上一行中数的个数的2倍,且第1行有1个数,
则前5行有1+2+4+8+16=31个数,则第6行中的第3个数为这个数列的第34个数,
即{an}这个数列的第34项,易得an=2n-1=2×34-1=67;
故答案为67.
点评:本题考查归纳推理,解题的关键要结合等差数列、等比数列的性质,进行分析解题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
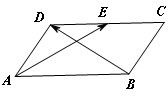 (2011•温州一模)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则
(2011•温州一模)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则