题目内容
已知等差数列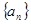 (
(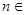 N+)中,
N+)中,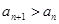 ,
,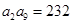 ,
,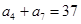 .
.
(Ⅰ)求数列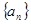 的通项公式;
的通项公式;
(Ⅱ)若将数列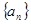 的项重新组合,得到新数列
的项重新组合,得到新数列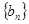 ,具体方法如下:
,具体方法如下: 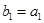 ,
,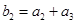 ,
,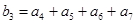 ,
,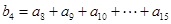 ,…,依此类推,
,…,依此类推,
第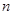 项
项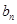 由相应的
由相应的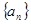 中
中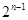 项的和组成,求数列
项的和组成,求数列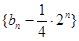 的前
的前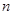 项和
项和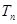 .
.
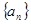 (
(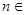 N+)中,
N+)中,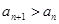 ,
,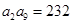 ,
,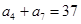 .
. (Ⅰ)求数列
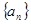 的通项公式;
的通项公式;(Ⅱ)若将数列
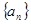 的项重新组合,得到新数列
的项重新组合,得到新数列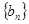 ,具体方法如下:
,具体方法如下: 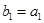 ,
,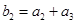 ,
,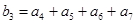 ,
,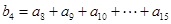 ,…,依此类推,
,…,依此类推,第
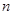 项
项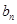 由相应的
由相应的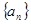 中
中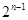 项的和组成,求数列
项的和组成,求数列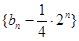 的前
的前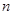 项和
项和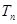 .
.(1)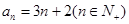 ;
;
(2)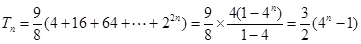 .
.
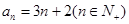 ;
;(2)
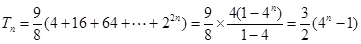 .
.(1)由等差数列的性质得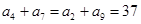 ,又
,又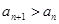 ,
,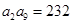 ,解得
,解得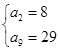 利用等差数列的通项公式得
利用等差数列的通项公式得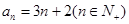 ;(2)根据数列
;(2)根据数列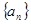 与新数列
与新数列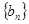 的关系转化为求等差数列的和得
的关系转化为求等差数列的和得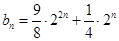 ,所以
,所以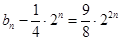 ,由等比数列求和公式得
,由等比数列求和公式得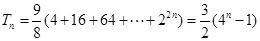 。
。
解:(Ⅰ)由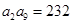 与
与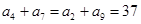
解得: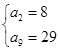 或
或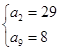 (由于
(由于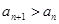 ,舍去)
,舍去)
设公差为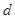 ,则
,则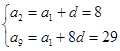 ,解得
,解得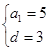
所以数列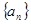 的通项公式为
的通项公式为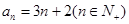 ……………………………………4分
……………………………………4分
(Ⅱ)由题意得:
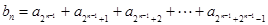
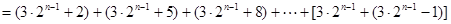
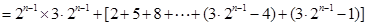 …………………………6分
…………………………6分
而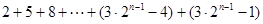 是首项为
是首项为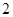 ,公差为
,公差为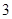 的等差数列的前
的等差数列的前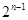 项的和,所以
项的和,所以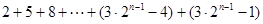
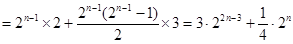
所以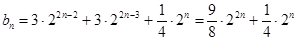 ………………………………10分
………………………………10分
所以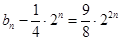
所以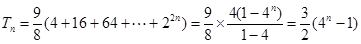 ……………………12分
……………………12分
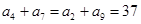 ,又
,又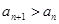 ,
,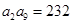 ,解得
,解得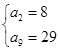 利用等差数列的通项公式得
利用等差数列的通项公式得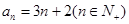 ;(2)根据数列
;(2)根据数列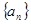 与新数列
与新数列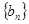 的关系转化为求等差数列的和得
的关系转化为求等差数列的和得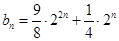 ,所以
,所以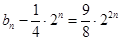 ,由等比数列求和公式得
,由等比数列求和公式得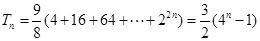 。
。解:(Ⅰ)由
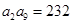 与
与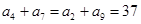
解得:
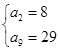 或
或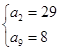 (由于
(由于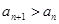 ,舍去)
,舍去)设公差为
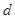 ,则
,则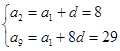 ,解得
,解得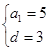
所以数列
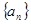 的通项公式为
的通项公式为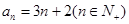 ……………………………………4分
……………………………………4分(Ⅱ)由题意得:
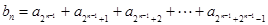
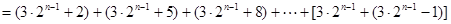
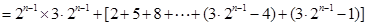 …………………………6分
…………………………6分而
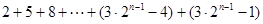 是首项为
是首项为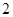 ,公差为
,公差为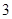 的等差数列的前
的等差数列的前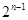 项的和,所以
项的和,所以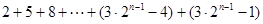
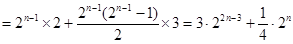
所以
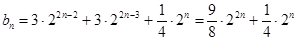 ………………………………10分
………………………………10分所以
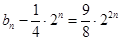
所以
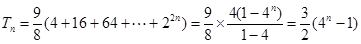 ……………………12分
……………………12分
练习册系列答案
相关题目
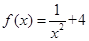 (x≠0),各项均为正数的数列
(x≠0),各项均为正数的数列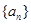 中
中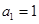 ,
,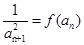 ,
,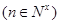 .
.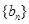 中,对任意的正整数
中,对任意的正整数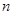 ,
, 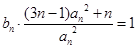 都成立,设
都成立,设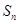 为数列
为数列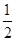 的大小.
的大小.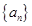 的前n项和为
的前n项和为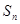 ,首项
,首项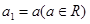 ,公差
,公差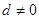 ,且
,且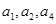 成等比数列。
成等比数列。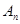 =
=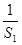 +
+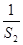 +
+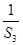 +…+
+…+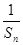 ,
, 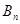 =
=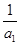 +
+ 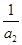 +
+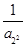 +… +
+… +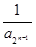 ,
,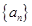 是以2为首项,1为公差的等差数列,数列
是以2为首项,1为公差的等差数列,数列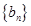 是以1为首项,2为公比的等比数列, 则
是以1为首项,2为公比的等比数列, 则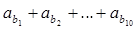 = .
= . 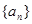 是等差数列,Sn是其前n项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( )
是等差数列,Sn是其前n项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( )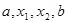 成等差数列,
成等差数列,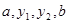 成等比数列,那么
成等比数列,那么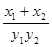 等于( )
等于( )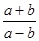
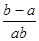
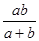
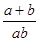
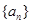 的前
的前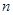 项和为
项和为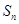 ,若
,若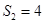 ,
,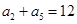 ,则
,则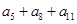 等于
等于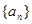 满足a1=1,且
满足a1=1,且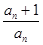 =
=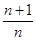 ,则
,则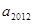 =( )
=( )