题目内容
设a>0为常数,已知函数f(x)=cos2(x-
)+sin2(x-
)+asin
cos
的最大值为3,求a的值.
| 2π |
| 3 |
| 5π |
| 6 |
| x |
| 2 |
| x |
| 2 |
分析:由倍角的公式、两角差的余弦公式化简解析式,再由平方关系将解析式转化为关于sinx的二次式,配方后求a的范围和正弦函数的值域求出此函数最大值,结合条件求解.
解答:解:由题意得f(x)=
+
+
sinx
=1+
(cos2xcos
+sin2xsin
)-
(cos2xcos
+sin2xsin
)+
sinx
=1-
cos2x+
sinx=1-
(1-2sin2x)+
sinx
=sin2x+
sinx+
=(sinx+
)2+
-
∵a>0,∴对称轴-
<0,
则当sinx=1时,f(x)取最大值为
,
由题意得
=3,解得a=3.
1+cos(2x-
| ||
| 2 |
1-cos(2x-
| ||
| 2 |
| a |
| 2 |
=1+
| 1 |
| 2 |
| 4π |
| 3 |
| 4π |
| 3 |
| 1 |
| 2 |
| 5π |
| 3 |
| 5π |
| 3 |
| a |
| 2 |
=1-
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
=sin2x+
| a |
| 2 |
| 1 |
| 2 |
=(sinx+
| a |
| 4 |
| 1 |
| 2 |
| a2 |
| 16 |
∵a>0,∴对称轴-
| a |
| 4 |
则当sinx=1时,f(x)取最大值为
| a+3 |
| 2 |
由题意得
| a+3 |
| 2 |
点评:本题考查了倍角的公式、两角差的余弦公式,平方关系,以及正弦函数的值域,二次函数的性质的应用,利用了整体思想和配方法.

练习册系列答案
相关题目
 )+sin2(x-
)+sin2(x- )+asin
)+asin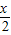 cos
cos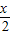 的最大值为3,求a的值.
的最大值为3,求a的值. ,
,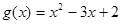 ,其中
,其中 ,a、b为常数,已知曲线
,a、b为常数,已知曲线 在点(2,0)处有相同的切线
在点(2,0)处有相同的切线 。
。 单调区间与极值。
单调区间与极值。