题目内容
曲线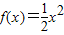
在点
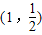处的切线方程为（ ）A．2x+2y+1=0
B．2x+2y-1=0
C．2x-2y-1=0
D．2x-2y-3=0
【答案】分析：对函数求导可得，然后求出函数在（1，
）的切线斜率k=f'（1），由点斜式求切线方程
解答：解：对函数求导可得，f'（x）=x
函数在（1，
）的切线斜率k=f'（1）=1，
由点斜式可得y-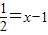
即2x-2y-1=0
故选C
点评：本题主要考查了导数的几何意义：函数在某点处的导数值即为改点的切线的斜率的应用，属于基础试题
）的切线斜率k=f'（1），由点斜式求切线方程解答：解：对函数求导可得，f'（x）=x
函数在（1，
）的切线斜率k=f'（1）=1，由点斜式可得y-
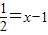即2x-2y-1=0故选C
点评：本题主要考查了导数的几何意义：函数在某点处的导数值即为改点的切线的斜率的应用，属于基础试题
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
（Ⅰ）求曲线
在点
处的切线方程；（Ⅱ）求函数
的单调区间；（Ⅲ）若函数
内单调递增，求
的取值范围.
，其中
在点
处的切线方程为
,求函数
的解析式；
，不等式
在
上恒成立，求实数b的取值范围。
，
在点
处
的切线方程；
的导数
满足
，
，其中常数
，求曲线
在点
处的切线方程.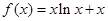
在点
处的切线方程为 .