Question

已知函数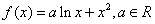

 (I)若a=-2，求证：函数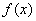在(1，+∞)上是增函数；

(II)当a≥-2时，求函数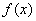在[1，e]上的最小值及相应的x值；

(Ⅲ)若存在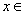[l，e]，使得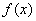≤(a+2)x成立，求实数a的取值范围．

Answer 1

（Ⅰ）当时,,当,,

故函数在上是增函数-

（Ⅱ）,当,,

当时,在上非负(仅当,x=1时,),

故函数在上是增函数,此时.

∴当时,的最小值为1,相应的x值为1.-

（Ⅲ）不等式,可化为.

∵, ∴且等号不能同时取,所以,即,

因而(),

令(),又,

当时,,,

从而(仅当x=1时取等号),所以在上为增函数,

故的最小值为,所以a的取值范围是.