题目内容
已知曲线
及点P（O，0），则过点P的曲线S的切线方程为 ．
【答案】分析：设出切点坐标，求出函数的导数，通过切线的斜率相等，求出切点坐标，然后求出切线方程，
解答：解：设曲线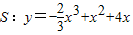
与过点P（0，0）的切线相切于点A（x，
），
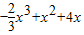则切线的斜率 k=y′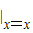
=-2x2+2x+4，
∴切线方程为y-（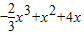
）=（-2x2+2x+4）（x-x），
∵点P（0，0）在切线上，
∴
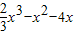=2x3-2x2-4x，即
x3-x2=0，
解得x=0或x=
，所以切线的斜率为：4或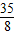
故所求的切线方程为：y=4x或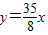
．
故答案为：y=4x或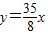
．
点评：此题考查学生会利用导数研究曲线上某点的切线方程，是一道综合题．学生在解决此类问题一定要分清“在某点处的切线”，还是“过某点的切线”；同时解决“过某点的切线”问题，一般是设出切点坐标解决．
解答：解：设曲线
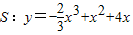与过点P（0，0）的切线相切于点A（x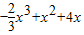，），则切线的斜率 k=y′
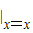=-2x2+2x+4，∴切线方程为y-（
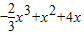）=（-2x2+2x+4）（x-x），∵点P（0，0）在切线上，
∴
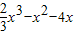=2x3-2x2-4x，即x3-x2=0，解得x=0或x=
，所以切线的斜率为：4或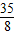故所求的切线方程为：y=4x或
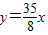．故答案为：y=4x或
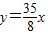．点评：此题考查学生会利用导数研究曲线上某点的切线方程，是一道综合题．学生在解决此类问题一定要分清“在某点处的切线”，还是“过某点的切线”；同时解决“过某点的切线”问题，一般是设出切点坐标解决．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
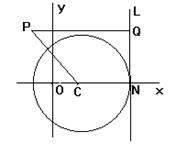
（2012•珠海二模）已知圆C方程：（x-1）2+y2=9，垂直于x轴的直线L与圆C相切于N点（N在圆心C的右侧），平面上有一动点P，若PQ⊥L，垂足为Q，且
；
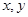轴的正半轴的交点，求四边形OADB的最大面积及D点坐标.
及点P（O，0），则过点P的曲线S的切线方程为________．