题目内容
△ABC的外接圆的圆心为O，两条边上的高的交点为H，| OH |
| OA |
| OB |
| OC |
分析：根据题意作出图形，由外心和垂心的性质证明四边形AHCD是平行四边形，由向量加法的三角形法则得
=
+
，由向量相等和向量的减法运算进行转化，直到用
、
和
表示出来为止．
| OH |
| OA |
| AH |
| OA |
| OB |
| OC |
解答：
解：如图：作直径BD，连接DA、DC，
由图得，
=-
，
∵H为△ABC的垂心，∴CH⊥AB，AH⊥BC，
∵BD为直径，∴DA⊥AB，DC⊥BC
∴CH∥AD，AH∥CD，故四边形AHCD是平行四边形，∴
=
又∵
=
-
=
+
，
∴
=
+
=
+
=
+
+
，对比系数得到m=1．
故答案为：1．
解：如图：作直径BD，连接DA、DC，由图得，
| OB |
| OD |
∵H为△ABC的垂心，∴CH⊥AB，AH⊥BC，
∵BD为直径，∴DA⊥AB，DC⊥BC
∴CH∥AD，AH∥CD，故四边形AHCD是平行四边形，∴
| AH |
| DC |
又∵
| DC |
| OC |
| OD |
| OC |
| OB |
∴
| OH |
| OA |
| AH |
| OA |
| DC |
| OA |
| OB |
| OC |
故答案为：1．
点评：本题考查了向量的线性运算的应用，一般的做法是根据图形找一个封闭的图形，利用向量的加法表示出来，再根据题意进行转化到用已知向量来表示，考查了转化思想．
练习册系列答案
相关题目
已知点A（0，1），B，C是x轴上两点，且|BC|=6（B在C的左侧）．设△ABC的外接圆的圆心为M．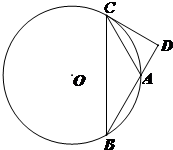
（2013•朝阳区一模）如图，圆O是△ABC的外接圆，过点C作圆O的切线交BA的延长线于点D．若
，试求直线AB的方程；
，试求s的最大值．