题目内容
已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.(Ⅰ)已知
 ,试求直线AB的方程;
,试求直线AB的方程;(Ⅱ)当圆M与直线y=9相切时,求圆M的方程;
(Ⅲ)设|AB|=l1,|AC|=l2,
 ,试求s的最大值.
,试求s的最大值.
【答案】分析:(Ⅰ)设出B,C的坐标,利用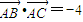 ,建立方程,求得B,C的坐标,从而可得直线AB的方程;
,建立方程,求得B,C的坐标,从而可得直线AB的方程;
(Ⅱ)设圆心为(a,b),半径为r,利用圆M与直线y=9相切,建立方程组,从而可求圆M的方程;
(Ⅲ)设B(m-3,0),C(m+3,0),求出|AB|=l1,|AC|=l2,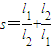 ,利用换元法、配方法即可求得结论.
,利用换元法、配方法即可求得结论.
解答:解:(Ⅰ)设B(a,0),则C(a+6,0).
∵A(0,1),∴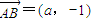 ,
, ,
,
由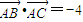 得a(a+6)+1=-4,
得a(a+6)+1=-4,
解得:a=-1或-5,
所以,直线AB的方程为
(Ⅱ)设圆心为(a,b),半径为r,则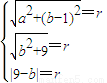 ,解之得:a=±4,b=4,r=5,
,解之得:a=±4,b=4,r=5,
所以,圆M的方程为(x±4)2+(y-4)2=25.
(Ⅲ)设B(m-3,0),C(m+3,0),则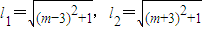 ,
,
所以,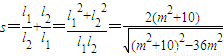
令m2+10=t(t≥10),则s=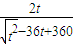 =
=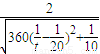 ≤
≤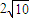
等号当且仅当t=20,即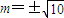 时取得.
时取得.
∴当 时,s的最大值为
时,s的最大值为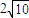
点评:本题考查向量知识的运用,考查圆的标准方程,考查最值的求解,正确列出函数关系式是关键.
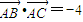 ,建立方程,求得B,C的坐标,从而可得直线AB的方程;
,建立方程,求得B,C的坐标,从而可得直线AB的方程;(Ⅱ)设圆心为(a,b),半径为r,利用圆M与直线y=9相切,建立方程组,从而可求圆M的方程;
(Ⅲ)设B(m-3,0),C(m+3,0),求出|AB|=l1,|AC|=l2,
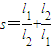 ,利用换元法、配方法即可求得结论.
,利用换元法、配方法即可求得结论.解答:解:(Ⅰ)设B(a,0),则C(a+6,0).
∵A(0,1),∴
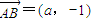 ,
, ,
,由
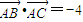 得a(a+6)+1=-4,
得a(a+6)+1=-4,解得:a=-1或-5,
所以,直线AB的方程为

(Ⅱ)设圆心为(a,b),半径为r,则
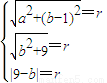 ,解之得:a=±4,b=4,r=5,
,解之得:a=±4,b=4,r=5,所以,圆M的方程为(x±4)2+(y-4)2=25.
(Ⅲ)设B(m-3,0),C(m+3,0),则
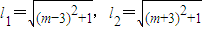 ,
,所以,
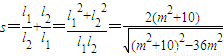
令m2+10=t(t≥10),则s=
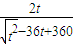 =
=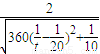 ≤
≤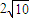
等号当且仅当t=20,即
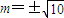 时取得.
时取得.∴当
 时,s的最大值为
时,s的最大值为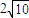
点评:本题考查向量知识的运用,考查圆的标准方程,考查最值的求解,正确列出函数关系式是关键.

练习册系列答案
相关题目
 已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.
已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.