题目内容
(本小题14分)
已知![]() 为平面直角坐标系的原点,过点
为平面直角坐标系的原点,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若![]() ,求直线
,求直线![]() 与圆的交点坐标.
与圆的交点坐标.
(本小题满分14分)
解:(Ⅰ)依题意,直线![]() 的斜率存在,
的斜率存在,
因为 直线![]() 过点
过点![]() ,可设直线
,可设直线![]() :
:![]() .
.
因为 ![]() ,圆的半径为1,
,圆的半径为1,![]() ,
,![]() 两点在圆
两点在圆![]() 上,
上,
所以 圆心![]() 到直线
到直线![]() 的距离等于
的距离等于![]() .
.
又因为 ![]() ,
,
所以 ![]() ,
,
所以 直线![]() 的方程为
的方程为![]() 或
或![]() . ………………………7分
. ………………………7分
(Ⅱ)设 ![]() ,
,![]() ,
,
所以 ![]() ,
,![]() .
.
因为 ![]() ,
,
所以 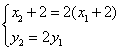 即
即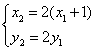 (*);
(*);
因为 ![]() ,
,![]() 两点在圆上,
两点在圆上,
所以 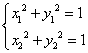 把(*)代入,得
把(*)代入,得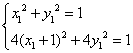 ,
,
所以 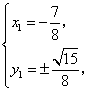
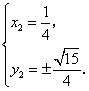
所以 ![]() 点坐标为
点坐标为![]() 或
或![]() ,
,![]() 点坐标为
点坐标为![]() 或
或![]() .
.
………………………14分

练习册系列答案
相关题目
 .
. ,点P为曲线
,点P为曲线 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程; 上为单调增函数,试求
上为单调增函数,试求 的取值范围.
的取值范围. 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1. =
=  .(其中
.(其中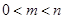 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数
 且函数
且函数 在区间
在区间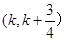 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ……
…… .
. ,x∈[1,+∞
,x∈[1,+∞
 时,求函数f(x)的最小值
时,求函数f(x)的最小值 
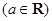 .
. ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; ,若对任意
,若对任意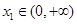 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。