题目内容
(本小题14分)已知二次函数 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1.
⑴ 求此二次函数 的解析式;
的解析式;
⑵ 若函数 的定义域为
的定义域为 =
=  .(其中
.(其中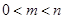 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数 的值域也为
的值域也为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)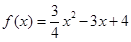 (2)存在满足条件的
(2)存在满足条件的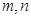 ,其中
,其中
【解析】
试题分析:(1)因为二次函数的最小值为1,所以可设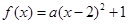 ,
,
因 ,代入得
,代入得 ,
,
所以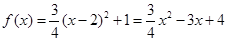 .
……4分
.
……4分
(2)假设存在这样的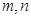 ,分类讨论如下:
,分类讨论如下:
①当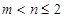 时,依题意有
时,依题意有 ,即
,即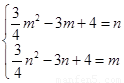 ,
,
两式相减,整理得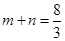 ,代入进一步得
,代入进一步得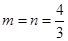 ,产生矛盾,故舍去;
……7分
,产生矛盾,故舍去;
……7分
②当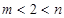 时,依题意
时,依题意 ,
,
若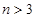 ,
,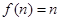 ,解得
,解得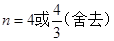 ,
,
若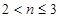 ,
,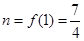 ,产生矛盾,故舍去,
……10分
,产生矛盾,故舍去,
……10分
③当 时,依题意,
时,依题意,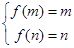 ,即
,即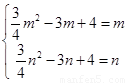 ,
,
解得 产生矛盾,故舍去;
……13分
产生矛盾,故舍去;
……13分
综上:存在满足条件的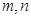 ,其中
,其中 。
……14分
。
……14分
考点:本小题主要考查二次函数解析式的求解和含参数的二次函数值域的求法,考查学生分类讨论思想的应用和运算求解能力.
点评:二次函数有一般式、顶点式和两根式三种形式,要根据题意选择合适的形式,分类讨论时要尽量做到不重不漏.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
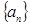 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使  成立的正整数
成立的正整数 的最小值.
的最小值. ,设
,设 。
。 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的图像与函数
的图像与函数 的图像关于点
的图像关于点 对称
对称 ,
, 在区间
在区间 上的值不小于6,求实数a的取值范围.
上的值不小于6,求实数a的取值范围. 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数 在D上的最小值,
在D上的最小值, 表示函数
表示函数 对任意的
对任意的 成立,则称函数
成立,则称函数 上的“k阶收缩函数”
上的“k阶收缩函数” ,试写出
,试写出 ,
, 的表达式;
的表达式; 试判断
试判断 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围